En la teoría financiera moderna, evaluar el rendimiento de la inversión a menudo se extiende más allá del análisis tradicional del rendimiento medio y la desviación estándar. Si bien métricas establecidas como el Ratio de Sharpe se basan en la suposición de una distribución normal de los rendimientos, los datos del mercado del mundo real—particularmente para activos digitales como Bitcoin (BTC)—frecuentemente exhiben asimetría y "colas gruesas." El Ratio Omega ofrece un enfoque fundamentalmente diferente al utilizar toda la distribución acumulativa de los rendimientos para distinguir el potencial de beneficio del riesgo de pérdida en relación con un umbral definido.
1. Definición y Fundamentos Matemáticos
Según la investigación de Kapsos et al. (2011), el Ratio Omega permite a los analistas evaluar la probabilidad de alcanzar un retorno objetivo específico al integrar toda la densidad de probabilidad. El ratio se define como la relación entre ganancias ponderadas por probabilidad y pérdidas ponderadas por probabilidad en un umbral de Retorno Mínimo Aceptable (MAR).
La representación matemática de Omega (Ω) se deriva a través de la Función de Distribución Acumulativa (CDF):
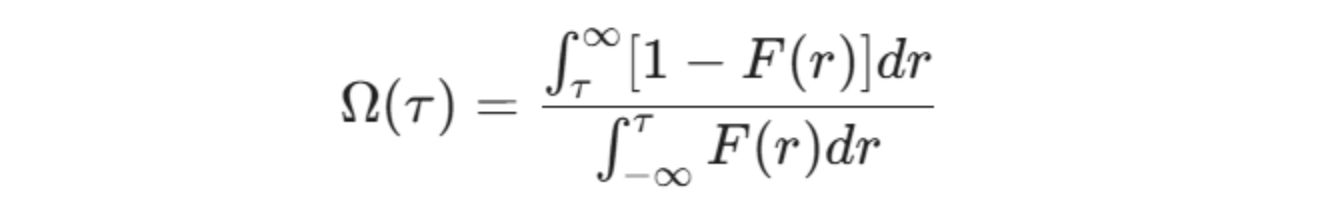
Dónde:
Ω: El Ratio Omega.
𝞃 (tau): El umbral de Retorno Mínimo Aceptable (MAR) definido por el inversor.
F(r): La Función de Distribución Acumulativa (CDF) de los retornos del activo.
r: El retorno del activo.
A través de la integración por partes, la ecuación se puede presentar en una forma más aplicable computacionalmente basada en valores esperados. Esto determina la masa de la distribución de retornos por encima del umbral [𝞃, +∞] (retorno positivo relativo a 𝞃) y por debajo del umbral [-∞, 𝞃] (retorno negativo relativo a 𝞃):
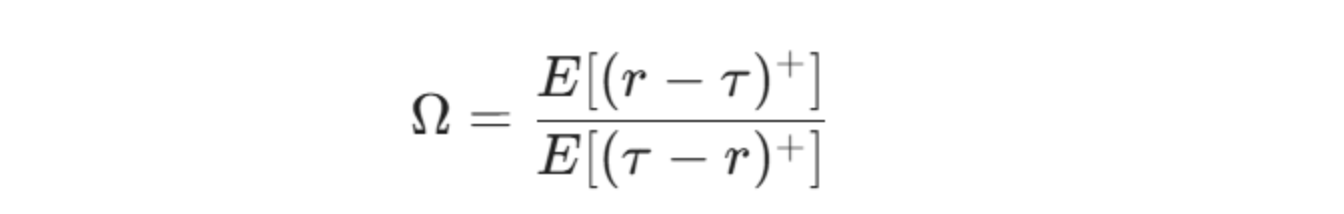
Dónde:
E[(r - 𝞃)+]: El valor esperado de las ganancias por encima del umbral 𝞃.
E[(𝞃 - r)+]: El valor esperado de las pérdidas por debajo del umbral 𝞃.
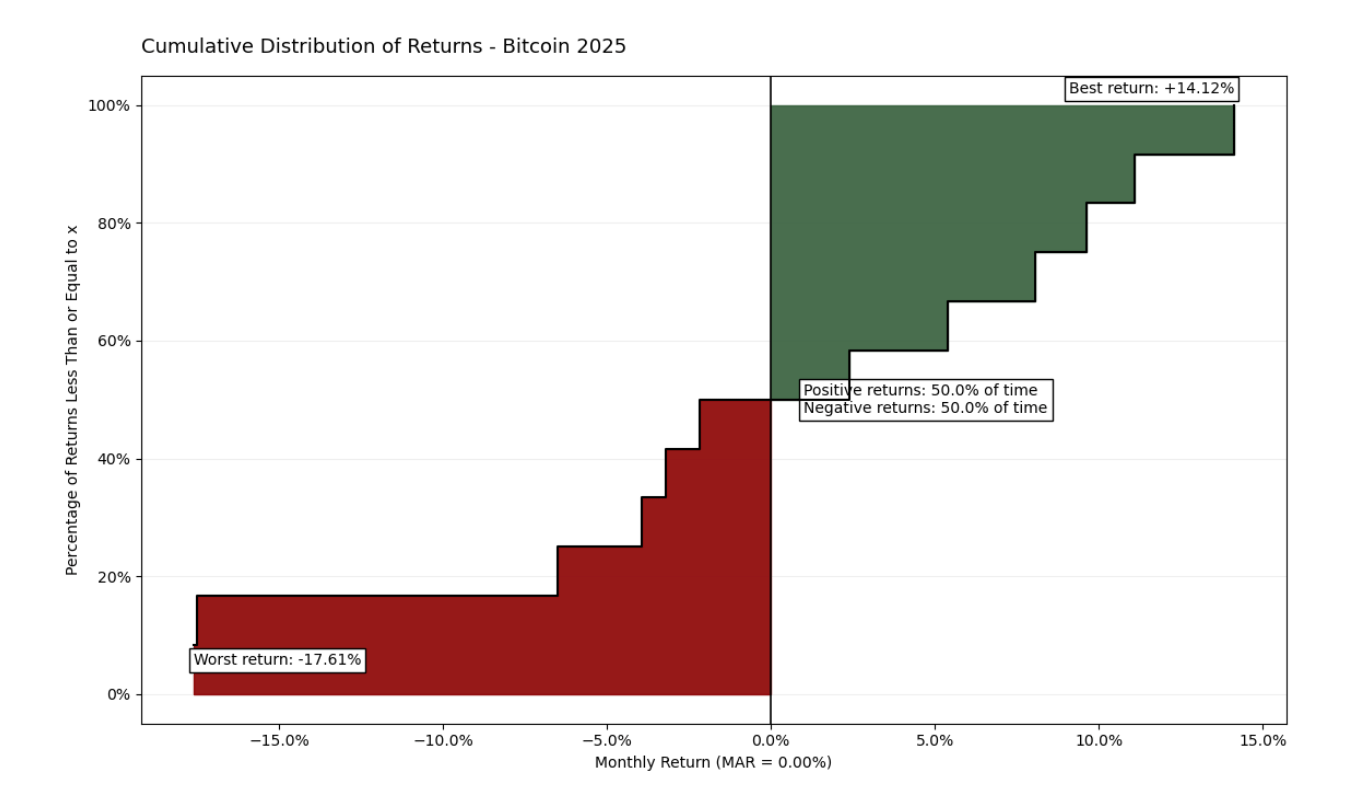
Los datos de 2025 ilustran la volatilidad asimétrica del activo, con fluctuaciones extremas que oscilan entre -17.61% y +14.12%. A pesar de una frecuencia equilibrada (50% meses positivos vs. 50% meses negativos), un Ratio Omega de 0.778 revela un peso mayor de las pérdidas en la cola izquierda de la curva. Esta paridad visual enfatiza que la magnitud de los descensos domina los repuntes, sirviendo como base fundamental para evaluar la calidad del activo en relación con el MAR elegido.
Si bien un gráfico de un año puede parecer voluminoso y menos informativo, expandir el horizonte temporal a un período de 10 años proporciona una imagen significativamente más completa.
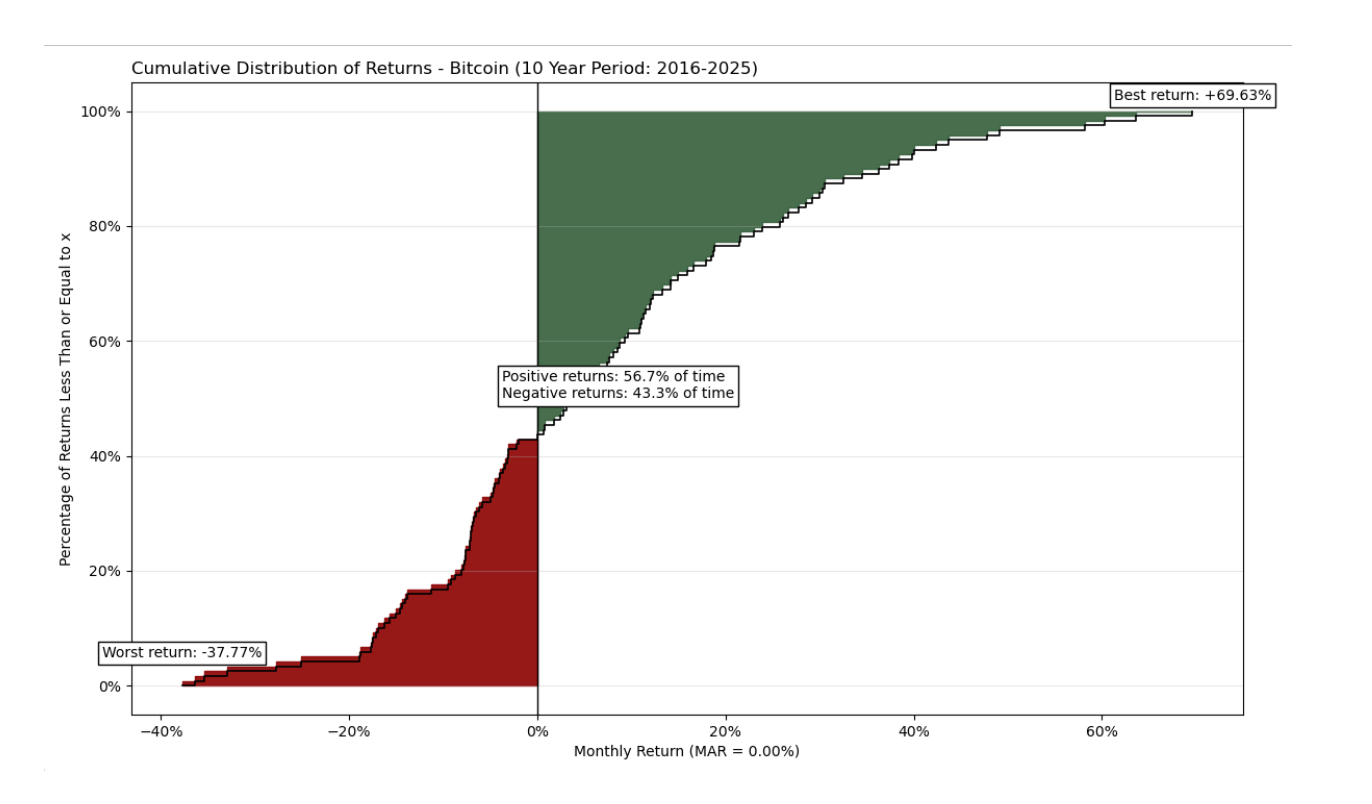
El análisis de 10 años revela un perfil de riesgo-retorno mucho más favorable. Aunque el activo retiene una volatilidad extrema con descensos mensuales tan bajos como -37.77%, demuestra un potencial de crecimiento impresionante con picos de hasta +69.63%. A diferencia de la instantánea de un año, los meses positivos dominan aquí (56.7% del tiempo), y la "zona verde" de ganancias visual y matemáticamente supera la "zona roja" de riesgo. El Ratio Omega para este período es 1.621, demostrando que Bitcoin genera una prima significativa en relación con el riesgo asumido a largo plazo.
2. Interpretación y Análisis de Riesgo
A diferencia de otros coeficientes, el valor de Omega depende directamente del umbral elegido 𝞃. Esto hace que la métrica sea adaptable al perfil de riesgo específico del inversor.
Ω > 1: Indica que el valor acumulado de las ganancias excede al de las pérdidas en relación con el MAR elegido. Un número más alto significa mejor calidad de retornos.
Ω = 1: Significa que el retorno esperado del activo es exactamente igual al umbral 𝞃.
Ω < 1: Indica que el riesgo de pérdida por debajo de la "barra" elegida supera el potencial de ganancia.
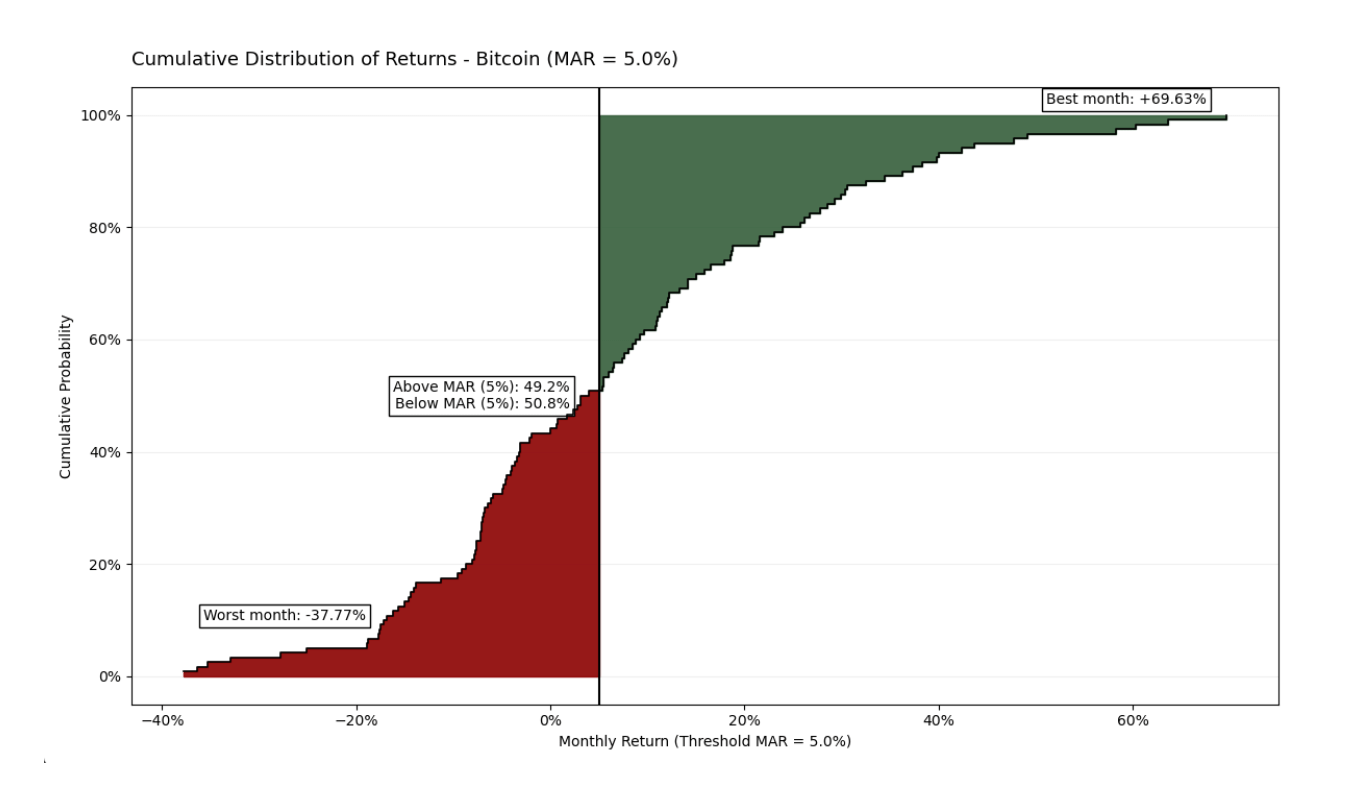
En el período de 10 años analizado, aplicar un MAR del 5% mensual coloca al activo en un marco más estricto. Aunque Bitcoin se mantiene por debajo de este umbral el 50.8% del tiempo, su Ratio Omega sigue siendo positivo en 1.2102. Esto confirma que la contribución de los meses "explosivos" (alcanzando hasta +69.63%) es lo suficientemente poderosa como para superar el efecto acumulativo de los meses con retornos negativos o mediocres. Los datos demuestran que incluso bajo altas expectativas de inversión, Bitcoin mantiene su ventaja estadística a largo plazo.
3. Optimización a través de Programación Lineal
Una de las aplicaciones prácticas más significativas del Ratio Omega, detallada por Kapsos et al. (2011), es su uso en la construcción activa de carteras. Si bien la función puede parecer inicialmente compleja de calcular, los autores demuestran que maximizar Omega puede reformularse como un problema de programación lineal.
El análogo discreto de Omega para fines computacionales sobre $m$ observaciones históricas es:
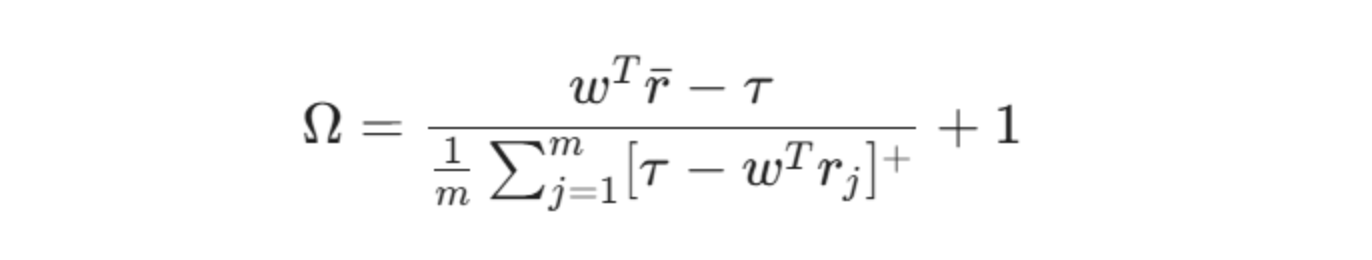
Dónde:
𝑤: Vector de pesos de activos en la cartera.
r: Vector de retornos históricos medios.
m: Número de observaciones históricas (muestras).
rj: Vector de retornos para cada observación específica ⅉ.
Este enfoque es fundamentalmente diferente de la optimización tradicional de Markowitz (Media-Varianza). En lugar de simplemente minimizar la volatilidad (lo que penaliza los movimientos bruscos hacia arriba), el modelo Omega permite a los inversores de Bitcoin optimizar sus posiciones para maximizar la "cola superior" de la distribución. Al sumar uno al ratio de retorno neto en exceso a la caída media, la fórmula de Kapsos permite que los algoritmos encuentren rápida y eficientemente los pesos (𝑤) que ofrecen la mejor probabilidad de éxito en relación con los objetivos individuales del inversor.
4. Análisis Comparativo: Bitcoin vs. S&P 500
Para entender el verdadero valor del Ratio Omega, es necesario comparar Bitcoin con un punto de referencia tradicional como el índice S&P 500. Las métricas de riesgo tradicionales como la desviación estándar a menudo fallan aquí porque no tienen en cuenta la asimetría y las diferencias en las estructuras de "cola" de las dos distribuciones.
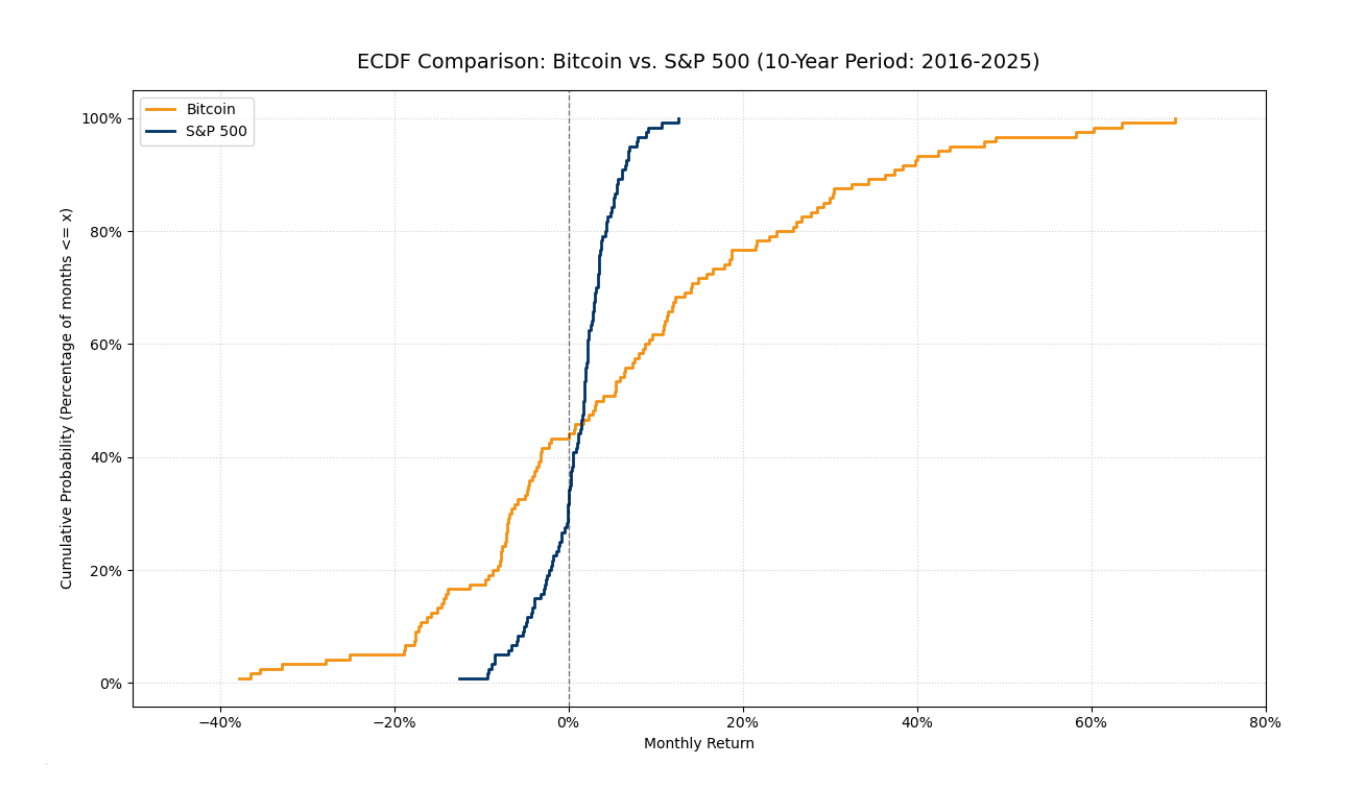
Este gráfico ECDF comparativo ilustra la diferencia fundamental entre los dos activos:
Concentración vs. Volatilidad: La línea del S&P 500 (azul oscuro) es significativamente más empinada y concentrada en un rango estrecho alrededor de cero. Esto indica un activo con menor volatilidad y una distribución más ajustada y predecible.
Las "Colas Gruesas" de Bitcoin: La línea de Bitcoin (naranja) demuestra extremos significativamente más amplios. Esta es una evidencia visual de "colas gruesas": una mayor probabilidad de desviaciones negativas y positivas masivas en comparación con el mercado tradicional.
Especificaciones de rendimiento: Mientras que el peor mes de Bitcoin alcanzó -37.77%, el activo generó con éxito períodos de crecimiento explosivo de hasta +69.63%. Estos saltos asimétricos en la "cola derecha" son la razón por la que Bitcoin a menudo genera un Ratio Omega mucho más alto a niveles de MAR más bajos.
Conclusión: La comparación confirma que Omega es una métrica de riesgo más justa que la desviación estándar. Reconoce el alto potencial de Bitcoin sin ignorar sus características de "cola gruesa", mientras permite a los inversores aplicar la fórmula de optimización para equilibrar los pesos de la cartera (𝑤) en relación con un umbral de retorno deseado (𝞃).
Conclusión Final
El análisis a través del Ratio Omega demuestra que las métricas tradicionales como el Ratio Sharpe son insuficientes para activos con "colas gruesas" como Bitcoin. Si bien un período de un año puede ser engañoso, el horizonte de 10 años revela la dominancia estadística de las ganancias (Ω = 1.621). Incluso en un umbral alto de MAR = 5%, el activo mantiene su eficiencia (Ω = 1.2102) debido a la magnitud de sus valores atípicos positivos. La comparación con el S&P 500 destaca que Bitcoin ofrece una exposición única a la "cola derecha" de la distribución. Utilizando el modelo de Kapsos et al., se transforman estas ideas teóricas en una herramienta práctica para la optimización de carteras a través de programación lineal. En última instancia, el Ratio Omega proporciona una evaluación más honesta y adaptativa del riesgo, reconociendo el potencial de crecimiento explosivo.
Referencias
Kapsos, M., Zymler, S., Christofides, N., y Rustem, B. (2011). Optimizando el Ratio Omega utilizando Programación Lineal. Imperial College London.