Как zk-ASM может обеспечить безопасный и надежный Интернет
Оригинальный анализ исследования Web3.com Ventures
0xрышилософер
Примечание. Эта статья довольно технически насыщена и предполагает базовое концептуальное знакомство с zk-Proofs и/или zk-Rollups. Более общее введение в эти принципы можно найти здесь.

Введение
Доказательства с нулевым разглашением, в частности zk-SNARK (краткие неинтерактивные аргументы знаний), возможно, являются одной из наиболее важных технологий на передовых рубежах Web 3. Хотя большая часть внимания средств массовой информации и инвестиций в этой подобласти была сосредоточена на zk. - Свертывания, решения для масштабирования, которые обеспечивают масштабируемость блокчейнов L1, таких как Ethereum, — это ни в коем случае не единственное применение zk-SNARK. В этом эссе я подробно проанализирую концепцию ассемблерного кода с нулевым разглашением (или zkASM), оценю варианты его использования как в zk-Rollup, так и за его пределами, исследуя его теоретические возможности в переосмыслении известного нам Интернета.
Технические принципы
zk-ASM, как следует из названия, содержит две основные технические части: ZK и ASM. Часть ZK относится к zk-SNARK, или кратким неинтерактивным аргументам знаний, а часть ASM относится к ассемблерному коду. Чтобы понять потенциал zk-ASM, мы должны сначала понять теоретические основы обеих этих, казалось бы, загадочных концепций.
zk-СНАРК
zk-SNARK — это жемчужина zk-Proofs: они представляют собой краткое доказательство того, что определенное утверждение истинно, когда доказательство ничего не раскрывает о доказываемых данных. Например, предположим, что кто-то утверждает утверждение: «Я знаю m такое, что C(m) = 0», где m — сообщение длиной в гигабайт, а C — функция. Zk-SNARK будет очень коротким доказательством (< 1 ГБ), которое можно быстро проверить и в котором ничего о m не раскрывается (кроме общедоступной информации) [1].
Так что же это за «С(м)»? Насколько это полезно? Эта функция на самом деле представляет собой арифметическую схему или представление направленного ациклического графа (DAG) конкретной функции, которую мы хотим выполнить, как показано на диаграмме [2]. «m» — это, по сути, входные данные в схему, а конкретные «узлы» в схеме — это отдельные логические элементы или арифметические операции. Например, узел «+» может иметь «2» и «3» в качестве входных данных и выводить «5» для следующего оператора. Таким образом, произвольная арифметическая или логическая операция может быть закодирована в «арифметической схеме».
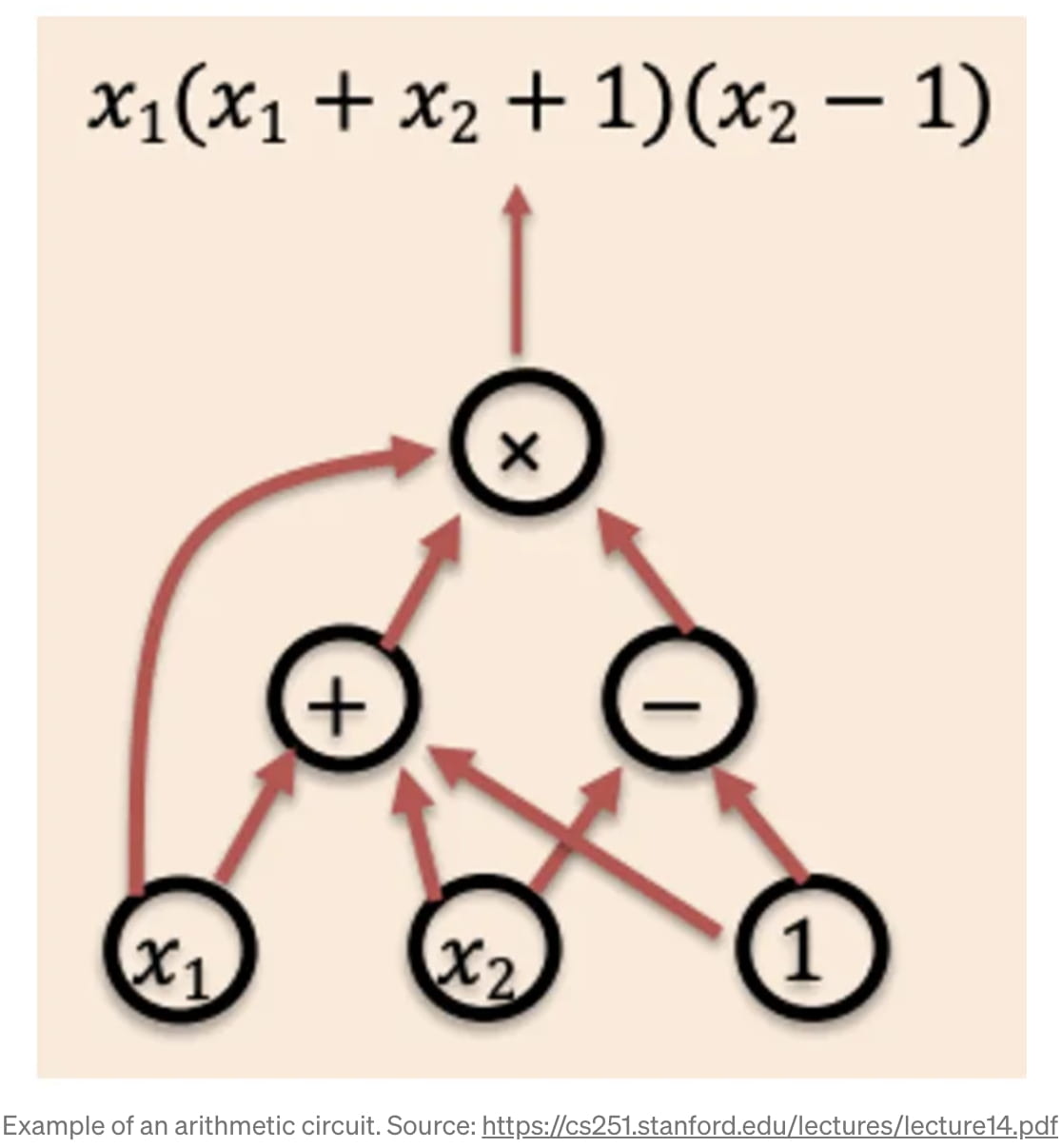
Как только у нас будет эта арифметическая схема как представление кода, на котором мы хотим запустить zk-SNARK, мы можем начать создавать этот zk-SNARK. По сути, zk-SNARK возможен благодаря «фундаментальной теореме алгебры», которая утверждает, что многочлен степени «d» имеет не более «d» корней [3]. Математический трюк состоит из двух шагов: (1) каким-то образом преобразовать функцию «f(m)», которую мы хотим доказать, в многочлен (и придерживаться этого), и (2) использовать «фундаментальную теорему алгебры» для взаимодействия с полиномом и дайте краткое доказательство. На техническом жаргоне первая часть называется «Схемой полиномиальных обязательств» (PCS), а вторая часть — «Полиномиальным интерактивным доказательством Oracle» (PIOP) [4].
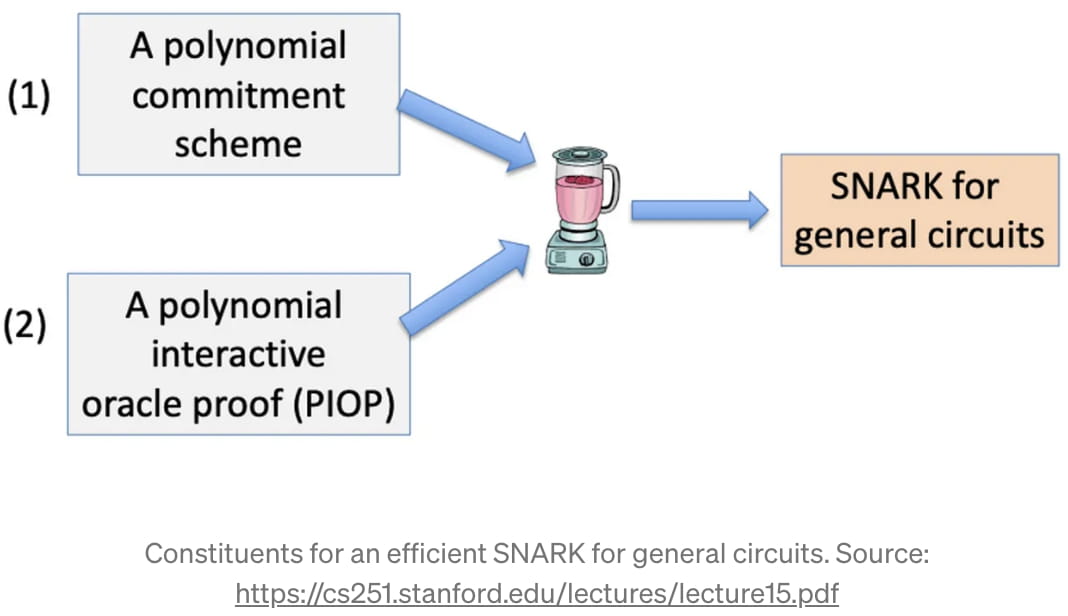
Хотя конкретные реализации PCS и PIOP выходят за рамки этой статьи, на данный момент мы получили приблизительный набросок основных этапов zk-SNARK:
У вас есть функция выбора (функция кода, математическое уравнение и т. д.), которую вы хотите запустить zk-SNARK.
Закодируйте эту функцию как арифметическую схему C(m)
Запустите PCS, чтобы получить полиномиальное представление этой арифметической схемы.
Запустите PIOP, чтобы получить краткое доказательство логарифмического размера исходного «m».
И, альт, у нас есть специально созданный zk-SNARK, который может доказать, что кто-то знает данное сообщение, не раскрывая, что это за сообщение.
Ассемблерный код
Вторая часть головоломки zk-ASM — это идея ассемблерного кода. Ассемблерный код — это класс языков, содержащий инструкции, написанные на очень низком языке, которые легко читать машине, но довольно сложно расшифровать человеку. В отличие от языков более высокого уровня, таких как Python, Java или даже C, языки Ассемблера содержат очень примитивные функции, такие как перемещение, сравнение, сложение и переход к ряду регистров данных в процессоре и жестко запрограммированных ячейках памяти. Например, код Python для вывода на экран чисел от 1 до 9: 123456789:

Довольно легко понять, не так ли? А вот его ассемблерная версия для x86 [5]:

Гораздо противнее, особенно для такой простой операции. Так зачем вообще использовать язык ассемблера? Как указано выше, хотя человеку может быть нелегко прочитать эти инструкции, их очень легко «собрать» в байт-код 110011001, который машина сможет читать и выполнять (это называется ассемблер) [6]. Для сравнения: языки более высокого уровня, такие как Python и Java, гораздо более удобны для чтения, но программы, написанные на этих языках, не могут быть напрямую выполнены процессором. Вместо этого нам нужно полагаться на «компилятор», который пережевывает код Python или Java, который мы пишем, и выдает дамп ассемблерного кода, подобного приведенному выше, для сборки и выполнения машиной. Мы можем ожидать, что один и тот же фрагмент Python или Java будет бесперебойно работать на разных процессорах и в разных операционных системах, поскольку компилятор выполняет тяжелую работу, компилируя исходный код в язык ассемблера, специфичный для этого процессора или операционной системы.
Поскольку все языки компилируются в ассемблерный код (который сам компилируется в исполняемый двоичный файл), ассемблер по сути является «матерью всех языков». Теперь предположим, что мы можем превратить все операнды на языке Ассемблера (например, x86 или RISC-V) в представление арифметической схемы, так что мы можем предоставить доказательства zk-SNARK для всех операндов в этом Ассемблер. язык. Это означает, что мы теоретически способны предоставить zk-SNARK любой программы, написанной на произвольном языке высокого уровня (например, Python или Java), который компилируется в этот язык ассемблера. И именно поэтому нам нужно внимательно подумать о zk-ASM.
Практическое применение
Пакеты zk-EVM: Polygon zk-ASM
Одним из наиболее важных применений zk-ASM является создание совместимых с виртуальной машиной Ethereum zk-Rollup или zk-EVM. Zk-EVM невероятно важен для масштабируемости блокчейна, поскольку он позволяет программистам развертывать цепочку L2 на основе zk-Rollup без внесения значительных изменений (если таковые имеются) в их код [7]. В этой области zk-EVM компании Polygon является образцовым примером, демонстрирующим, как zk-ASM можно использовать для достижения этой цели.
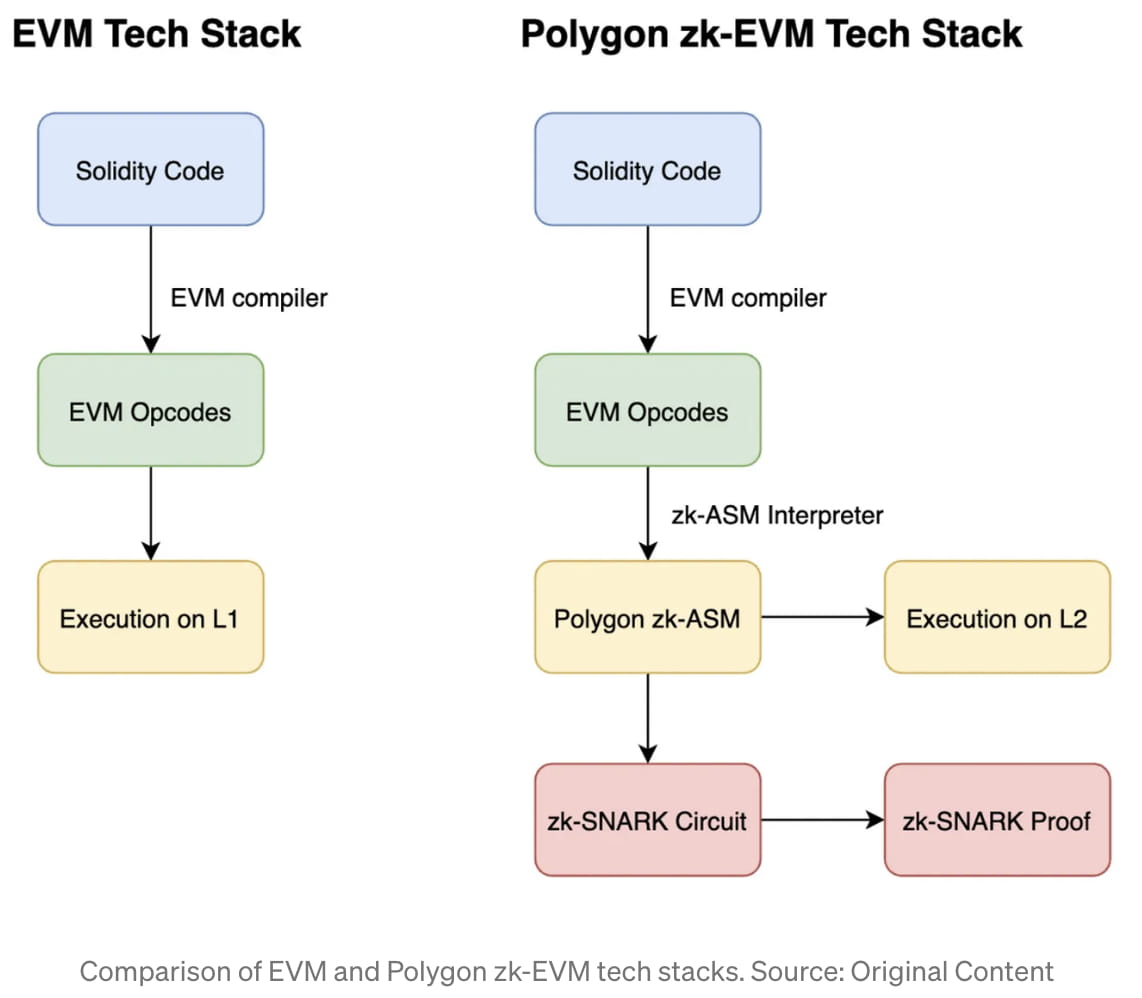
Когда программисты разрабатывают блокчейн Ethereum L1, они обычно пишут код на Solidity, языке высокого уровня, похожем на C. Этот код Solidity перед выполнением компилируется в серию кодов операций EVM, таких как ADD, SLOAD и EQ. на блокчейне L1 [8]. По умолчанию этот процесс, очевидно, не создает никаких zk-Proof. Хитрость Polygon заключается в том, чтобы создать метод для интерпретации каждого из кодов операций EVM в специально написанный zk-ASM, который очень дружелюбен к zk-SNARK. Затем их zk-EVM L2 выполнит zk-ASM, а также создаст схему zk-SNARK ASM для создания доказательства zk-SNARK [9]. Например, код операции ADD в EVM будет преобразован в zk-ASM Polygon следующим образом [10]:

Поскольку ловкость рук Polygon zk-EVM происходит на уровне сборки, от кода, с которым работает средний программист Ethereum, отделяют два уровня — уровень «Надежность». Именно по этой причине большинство разработчиков могут портировать свой код EVM, созданный для основной сети Ethereum, непосредственно на Polygon zk-EVM. Более того, поскольку Polygon zk-EVM «сохраняет» технологический стек Ethereum до уровня кода операции, вся инфраструктура отладки, основанная на анализе скомпилированных кодов операций, останется работоспособной и неповрежденной. Это отличается от некоторых других проектов zk-EVM, таких как zk-Sync, которые не обеспечивают zk-Proofs на уровне кода операции. Таким образом, даже несмотря на то, что Polygon изобретает и проверяет свой собственный язык ассемблера, Виталик пишет, что «он все еще может проверять код EVM, просто он использует для этого какую-то другую внутреннюю логику» [11].
За пределами накопительных пакетов: zk-WASM
zk-EVM — далеко не единственное применение zk-ASM. Вспомните наше предыдущее утверждение о том, что языки Ассемблера по сути являются «матерью всех языков» и что создание zk-ASM откроет возможности zk-Proofs для общих программ, написанных на любом языке, который компилируется в этот язык Ассемблера. Веб-сборка, или WASM, — один из наиболее важных новых языков ассемблера. Целью WASM, впервые опубликованной в 2018 году, является создание языка ассемблера, который увеличил бы скорость выполнения веб-приложений и обеспечил исполнительное дополнение к Javascript, основному языку кодирования, лежащему в основе Интернета [12].
По сути, по мере развития Интернета с годами растущий размер и сложность веб-приложений привели к тому, что браузеры часто невероятно медленно компилируют все, что написано на Javascript, и им приходится полагаться на сложные циклы компиляции-оптимизации-перезагрузки [12]. WebAssembly, с другой стороны, устраняет необходимость полагаться на сложные механизмы выполнения браузера, предоставляя переносимый, модульный и легко исполняемый язык ассемблера. Более того, будучи языком ассемблера, WASM позволяет программистам напрямую писать фрагменты кода на C, C++, Rust, Java или Ruby, которые автоматически запускаются в браузере. Таким образом, WASM стала предпочтительной технологией для «обеспечения распределенных бессерверных функций» [13].
Так почему и как на сцену выходят zk-SNARK? WASM уникален тем, что это клиентская технология, способная напрямую взаимодействовать с пользовательскими вводами и данными. Поскольку зачастую это включает в себя конфиденциальные данные, такие как пароли и личная информация, нам нужна технология, которая (1) гарантирует правильную работу программы и (2) утечку нашей конфиденциальной информации. Как описано выше, zk-SNARK является идеальным решением для решения обеих этих проблем и, таким образом, является важной частью головоломки в обеспечении безопасности WASM [14].
Хотя работа над разработкой zk-WASM все еще находится на ранней стадии, в последнее время появилось несколько проектов, которые выпустили прототипы схем zk-SNARK для WebAssembly. Например, эмулятор zk-SNARK «ZAWA» от Delphinus Lab представляет метод кодирования операндов и семантики виртуальной машины WASM в арифметическую схему, которая позволяет проводить доказательства zk-SNARK [13]. Со временем схемы zk-WASM, несомненно, будут постоянно оптимизироваться, что позволит программам, написанным на общих языках (таких как C, C++, Rust и Ruby), принять парадигму zk-Proofs.
Заключение
В этом эссе мы изучили теоретические основы zk-ASM, а также рассмотрели два парадигмальных примера использования zk-ASM: использование Polygon zk-ASM для создания zk-EVM на уровне кода операции, а также применение zk -SNARKs в WebAssembly для создания zk-WASM. В конечном итоге, zk-ASM обещает объединить совместимость и масштабируемость Web 2 с надежностью и безопасностью Web 3.
С одной стороны, блокчейны все чаще стремятся выйти за пределы своих нынешних узких мест в пропускной способности и потенциально поддерживать выполнение, в то время как, с другой стороны, методы Web 2 все чаще подвергаются атакам из-за неадекватной защиты пользовательских данных и конфиденциальности. Поскольку программисты могут использовать парадигмы проектирования Web 3 в своем коде Web 2 и вводить языки и код Web 2 в блокчейн, общие zk-ASM могут представлять собой точку слияния в мире Web 2 и Web 3 [15]. Именно в этом смысле zk-ASM может позволить нам переосмыслить более безопасный и не требующий доверия Интернет.
🐦 @0xfishylosopher
📅 17 декабря 2022 г.
Отказ от ответственности: информация, представленная выше, носит чисто образовательный характер и не представляет собой финансовую рекомендацию, а отражает точку зрения исключительно автора. Delphinus Lab — портфельная компания Web3.com Ventures.
Рекомендации
[1] https://z.cash/technology/zksnarks/
[2] https://cs251.stanford.edu/lectures/lecture14.pdf
[3] https://www.britannica.com/science/fundamental-theorem-of-algebra
[4] Создание эффективных SNARK: https://cs251.stanford.edu/lectures/lecture15.pdf.
[5] Пример из: https://www.tutorialspoint.com/assembly_programming/assembly_loops.htm.
[6] https://en.wikipedia.org/wiki/Assembly_language
[7] https://www.alchemy.com/overviews/zkevm
[8] Список кодов операций: https://ethereum.org/en/developers/docs/evm/opcodes/.
[9] https://wiki.polygon.technology/docs/zkEVM/zkASM/introduction
[10] https://wiki.polygon.technology/docs/zkEVM/zkASM/some-examples
[11] https://vitalik.ca/general/2022/08/04/zkevm.html
[12] https://blog.developer.adobe.com/understanding-webassembly-wasm-d5b592208ecc
[13] https://jhc.sjtu.edu.cn/~hongfeifu/manuscriptb.pdf
[14] https://hyperoracle.medium.com/zkwasm-the-next-chapter-of-zk-and-zkvm-471038b1fba6
[15] https://delphinuslab.com/zk-wasm/