Como o zk-ASM pode fornecer uma internet segura e confiável
Análise de pesquisa original da Web3.com Ventures
0xPeixe-ilósofo
Nota: Este artigo é uma peça bastante densa tecnicamente e pressupõe familiaridade conceitual básica com zk-Proofs e/ou zk-Rollups. Uma introdução mais geral a esses princípios pode ser encontrada aqui.

Introdução
Provas de Conhecimento Zero, em particular zk-SNARKs (Succinct Non-interactive Arguments of Knowledge) é talvez uma das tecnologias mais importantes nas fronteiras da Web 3. Enquanto a maior parte da atenção da mídia e do investimento neste subcampo foi para zk-Rollups, soluções de escala que fornecem magnitudes de escalabilidade para blockchains L1 como Ethereum, esta não é de forma alguma a única aplicação de zk-SNARKs. Neste ensaio, analisarei em profundidade o conceito de código Zero-Knowledge Assembly (ou zkASM), avaliando seus casos de uso em zk-Rollups e além, explorando suas possibilidades teóricas na reinvenção da Internet como a conhecemos.
Princípios técnicos
O zk-ASM, como o próprio nome sugere, contém duas partes técnicas principais: ZK e ASM. A parte ZK se refere a zk-SNARKs, ou Succinct Non-Interactive Arguments of Knowledge, enquanto a parte ASM se refere ao código Assembly. Para entender o potencial do zk-ASM, precisamos primeiro entender os fundamentos teóricos desses dois conceitos aparentemente arcanos.
zk-SNARKs
zk-SNARKs são as joias da coroa das zk-Proofs: elas são uma prova sucinta de que uma determinada afirmação é Verdadeira, onde a prova não revela nada sobre os dados que estão sendo provados. Por exemplo, considere alguém afirmando a afirmação “Eu conheço um m tal que C(m) = 0”, onde m é uma mensagem de um gigabyte de comprimento e C é uma função. Um zk-SNARK seria uma prova muito curta (< 1 GB) que pode ser rapidamente verificada e uma onde nada sobre m é revelado (além das informações disponíveis publicamente) [1].
Então o que é esse “C(m)”? Como ele é útil? Essa função é na verdade um circuito aritmético, ou uma representação de Grafo Acíclico Direcionado (DAG) de uma função específica que queremos executar, como mostra o diagrama [2]. O “m” é essencialmente os dados de entrada no circuito, e “nós” específicos no circuito são portas lógicas individuais ou operações aritméticas. Por exemplo, um nó “+” pode ter “2” e “3” como entradas, e gerar um “5” para o próximo operador. Assim, uma operação aritmética ou lógica arbitrária pode ser codificada em um “circuito aritmético”.
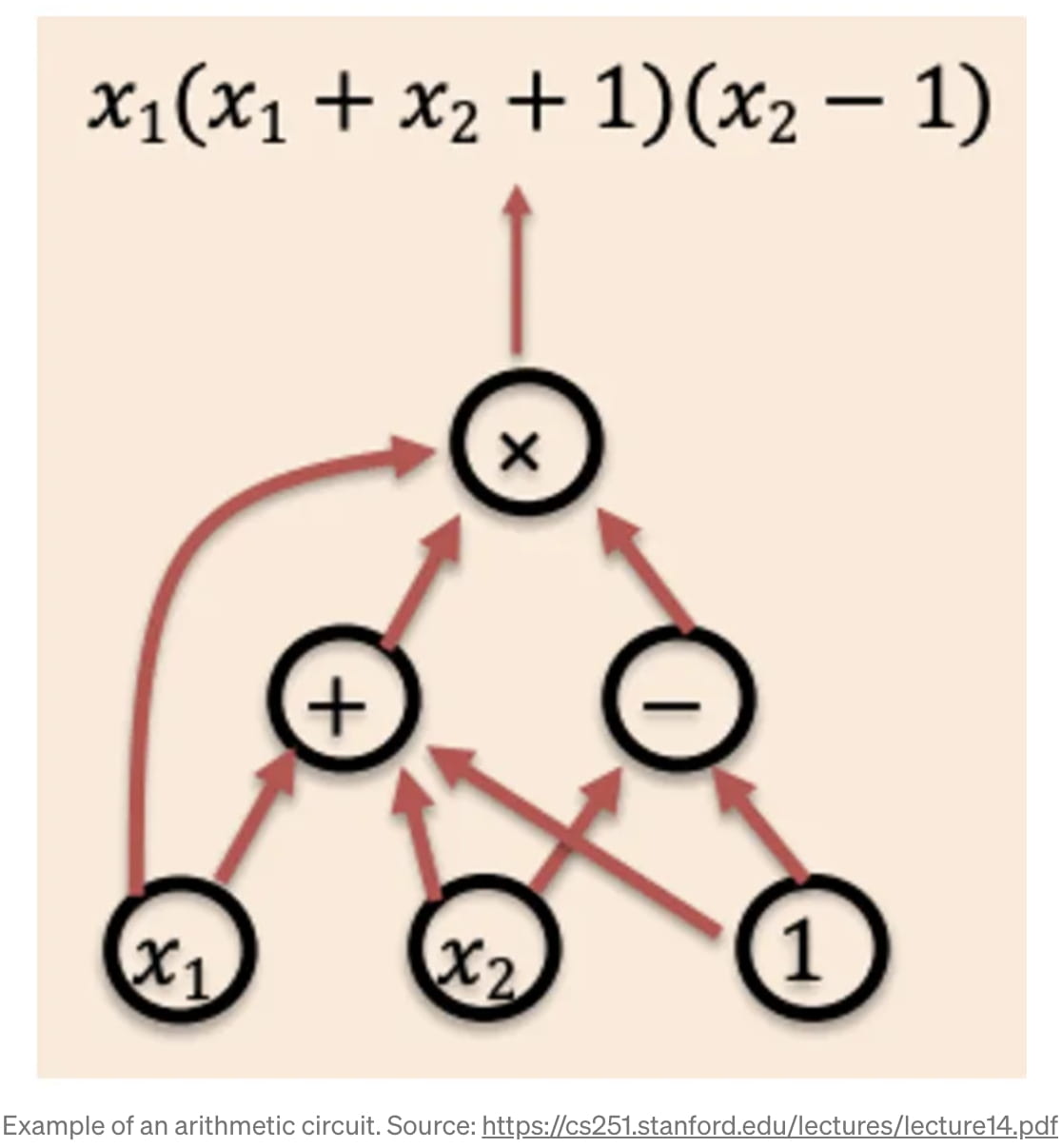
Uma vez que temos esse circuito aritmético como uma representação do código no qual queremos executar um zk-SNARK, podemos começar a construir esse zk-SNARK. Fundamentalmente, um zk-SNARK é possível por causa do “teorema fundamental da álgebra”, que afirma que um polinômio de grau “d” tem no máximo “d” raízes [3]. O truque matemático são duas etapas: (1) converter de alguma forma a função “f(m)” que queremos provar em um polinômio (e ficar com isso), e (2) usar o “teorema fundamental da álgebra” para interagir com o polinômio e fornecer uma prova sucinta. No jargão técnico, a primeira parte é chamada de “Esquema de Compromisso Polinomial” (PCS), e a segunda parte é chamada de “Prova Interativa de Oráculo Polinomial” (PIOP) [4].
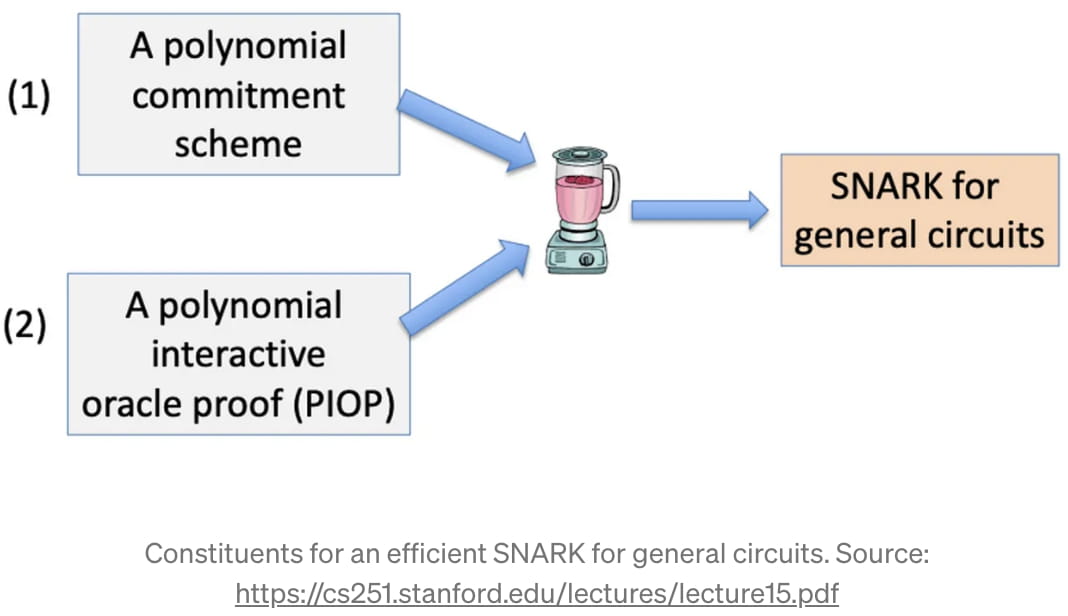
Embora as implementações específicas de um PCS e PIOP estejam além do escopo deste artigo, até agora derivamos um esboço das etapas principais de um zk-SNARK:
Tenha uma função de escolha (função de código, equação matemática etc.) que você deseja executar um zk-SNARK
Codifique esta função como um circuito aritmético C(m)
Execute um PCS para obter uma representação polinomial deste circuito aritmético
Execute um PIOP para obter uma prova logarítmica sucinta em tamanho para o “m” original
E pronto, temos um zk-SNARK personalizado que pode provar que alguém conhece uma determinada mensagem sem revelar qual é essa mensagem.
Código de montagem
A segunda peça do quebra-cabeça do zk-ASM é a ideia de Código Assembly. Código assembly é uma classe de linguagens que contém instruções de linguagem muito baixa que são fáceis para uma máquina ler, mas bastante difíceis para um humano decifrar. Ao contrário de linguagens de nível superior, como Python, Java ou mesmo C, as linguagens Assembly contêm funções muito primitivas, como mover, comparar, adicionar e pular em uma série de registradores de dados no processador e locais de memória codificados. Por exemplo, o código Python para imprimir os números de 1 a 9 na tela é 123456789:

Bem fácil de entender, certo? Agora aqui está a versão x86 Assembly dele [5]:

Muito mais desagradável, especialmente para uma operação tão simples. Então por que usar a linguagem Assembly? Conforme declarado acima, embora essas instruções possam não ser fáceis de ler para um humano, elas são muito fáceis de “montar” no byte-code 110011001 para uma máquina ler e executar (isso é chamado de assembler) [6]. Comparativamente falando, linguagens de nível superior como Python e Java são muito mais amigáveis para humanos lerem, mas programas escritos nessas linguagens não podem ser executados diretamente por um processador. Em vez disso, precisamos confiar em um “compilador” que mastiga o código Python ou Java que escrevemos e cospe um dump de código assembly como o acima para ser montado e executado pela máquina. Podemos esperar que o mesmo pedaço de Python ou Java rode suavemente em diferentes processadores e diferentes sistemas operacionais porque o compilador faz o trabalho pesado, compilando seu código-fonte em uma linguagem Assembly específica para aquele processador ou sistema operacional.
Como todas as linguagens compilam para código assembly (que por sua vez é compilado para binário executável), assembly é essencialmente como uma "mãe de todas as linguagens". Agora, suponha que somos capazes de transformar todos os operandos em uma linguagem Assembly (como x86 ou RISC-V) em uma representação de circuito aritmético, de modo que somos capazes de fornecer provas zk-SNARK de todos os operandos nesta linguagem Assembly. Isso significa que somos teoricamente capazes de fornecer um zk-SNARK de qualquer programa escrito em uma linguagem arbitrária de alto nível (como Python ou Java) que compila para esta linguagem Assembly. E é por isso que precisamos nos preocupar em pensar sobre zk-ASMs.
Aplicações práticas
zk-EVM Rollups: Polígono zk-ASM
Uma das aplicações mais importantes para o zk-ASM é na criação de zk-Rollups compatíveis com a Máquina Virtual Ethereum, ou zk-EVMs. Um zk-EVM é incrivelmente importante para a escalabilidade do blockchain porque permite que os programadores implantem em uma cadeia L2 baseada em zk-Rollup sem modificar muito (se houver) de seu código [7]. Neste campo, o zk-EVM da Polygon é um estudo de caso exemplar que demonstra como o zk-ASM pode ser usado para atingir esse objetivo.
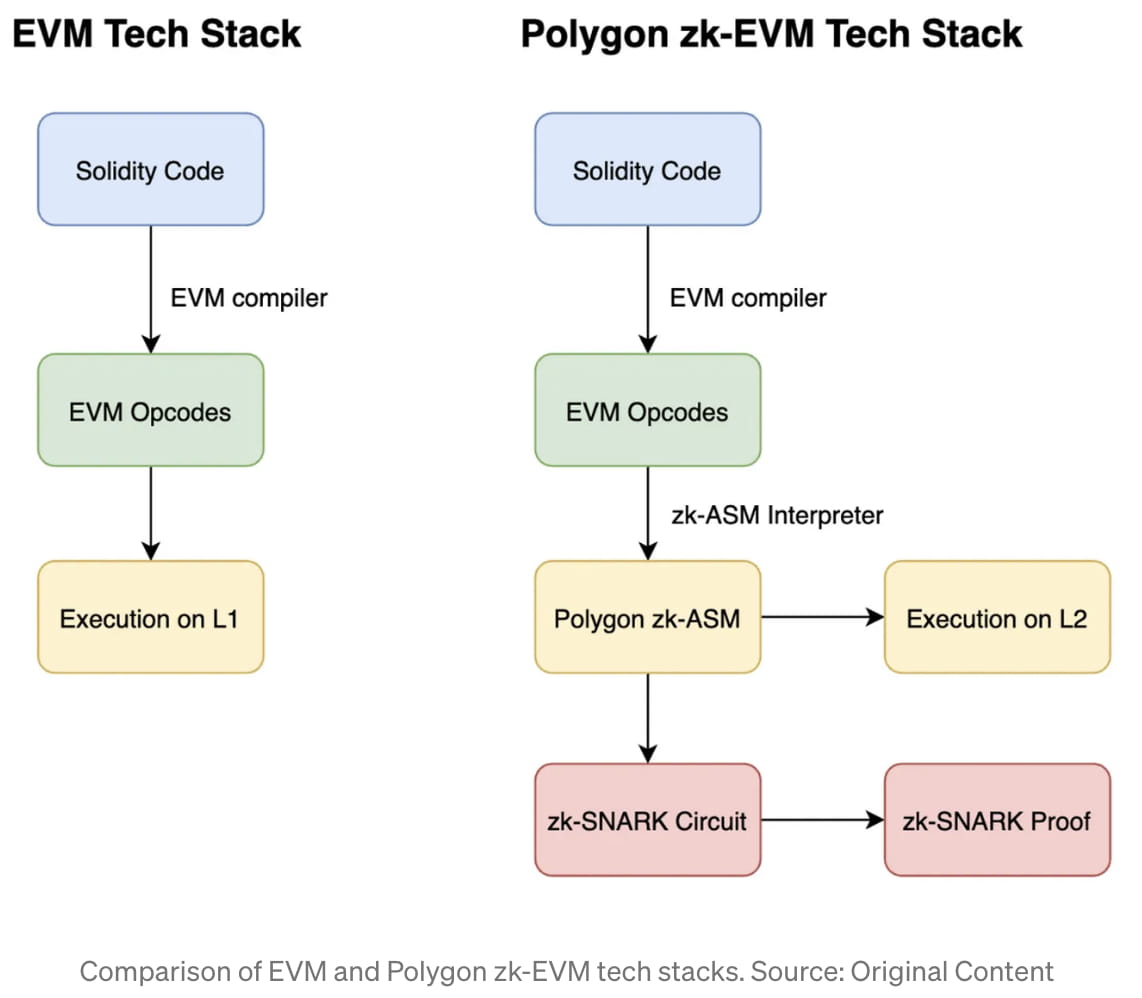
Quando os programadores desenvolvem na blockchain Ethereum L1, eles geralmente codificam em Solidity, que é uma linguagem de alto nível semelhante a C. Este código Solidity é compilado em uma série de Opcodes EVM, como ADD, SLOAD e EQ, antes de ser executado na blockchain L1 [8]. Por padrão, este processo obviamente não cria nenhum tipo de zk-Proof. O truque do Polygon é criar um método para interpretar cada um dos Opcodes EVM em seu zk-ASM personalizado, que é muito amigável ao zk-SNARK. Então, seu zk-EVM L2 executará o zk-ASM, enquanto também cria um circuito zk-SNARK do ASM para criar uma prova zk-SNARK [9]. Por exemplo, o opcode ADD na EVM será traduzido para o zk-ASM do Polygon da seguinte forma [10]:

Como o truque do Polygon zk-EVM acontece no nível Assembly, ele está a dois níveis de distância do código que o programador Ethereum médio toca, o nível “Solidez”. Esta é a razão pela qual a maioria dos desenvolvedores pode portar seu código EVM construído para a rede principal Ethereum diretamente para o Polygon zk-EVM. Além disso, como o Polygon zk-EVM “mantém” a pilha de tecnologia do Ethereum até o nível do opcode, toda a infraestrutura de depuração que depende da análise de opcodes compilados será mantida utilizável e intacta. Isso é diferente de alguns outros designs zk-EVM, como o zk-Sync, que não fornece zk-Proofs em um nível de opcode. Assim, mesmo que o Polygon invente e prove sua própria linguagem Assembly, Vitalik escreve que “ele ainda pode verificar o código EVM, ele apenas usa alguma lógica interna diferente para fazer isso” [11].
Além de Rollups: zk-WASM
zk-EVMs não são de forma alguma a única aplicação para zk-ASMs. Lembre-se de nossa afirmação anterior de que as linguagens Assembly são essencialmente “a mãe de todas as linguagens” e que a criação de um zk-ASM desbloqueará zk-Proofs para programas genéricos escritos em qualquer linguagem que compile para essa linguagem Assembly. Web Assembly, ou WASM, é uma das mais importantes linguagens assembly emergentes. Publicado pela primeira vez em 2018, o objetivo do WASM é criar uma linguagem Assembly que aumentasse a velocidade de execução de Web Apps e fornecesse um complemento de execução para Javascript, a principal linguagem de codificação por trás da Web [12].
Essencialmente, conforme a Web se desenvolveu ao longo dos anos, o tamanho e a complexidade crescentes dos Web Apps significaram que, muitas vezes, é incrivelmente lento para os navegadores compilarem tudo escrito em Javascript, e devem depender de ciclos complexos de compilação-otimização-recarregamento [12]. O WebAssembly, por outro lado, elimina a necessidade de depender de mecanismos complexos de execução de navegador, fornecendo uma linguagem assembly portátil, modular e facilmente executável. Além disso, como uma linguagem Assembly, o WASM permite que os programadores escrevam diretamente trechos de código em C, C++, Rust, Java ou Ruby que rodam nativamente em um navegador. O WASM, portanto, se tornou uma tecnologia de escolha para “fornecer funções distribuídas sem servidor” [13].
Então por que e como os zk-SNARKs entram em cena? O WASM é único por ser uma tecnologia do lado do cliente, capaz de interagir diretamente com entradas e dados do usuário. Como muitas vezes isso inclui dados confidenciais, como senhas e informações pessoais, precisamos de uma tecnologia que (1) garanta que o programa seja executado corretamente e que (2) nossas informações confidenciais não vazem. Conforme descrito acima, um zk-SNARK é uma solução perfeita para resolver esses dois problemas e, portanto, é uma peça importante do quebra-cabeça para proteger o WASM [14].
Embora o trabalho no desenvolvimento do zk-WASM ainda esteja em seus estágios iniciais, recentemente houve alguns projetos que lançaram circuitos protótipos zk-SNARK para WebAssembly. Por exemplo, o emulador zk-SNARK “ZAWA” do Delphinus Lab apresenta um método para codificar os operandos e a semântica de uma máquina virtual WASM em um circuito aritmético, o que lhe permite conduzir provas zk-SNARK [13]. Com o passar do tempo, os circuitos zk-WASM serão, sem dúvida, continuamente otimizados, permitindo assim que programas escritos em linguagens genéricas (como C, C++, Rust e Ruby) adotem o paradigma de zk-Proofs.
Conclusão
Ao longo deste ensaio, exploramos os fundamentos teóricos do zk-ASM, bem como examinamos dois estudos de caso paradigmáticos do zk-ASM: o uso do zk-ASM pelo Polygon para criar um zk-EVM de nível de opcode, bem como a aplicação de zk-SNARKs no WebAssembly para criar o zk-WASM. Em última análise, a promessa do zk-ASM é unir a interoperabilidade e a escala da Web 2 com a falta de confiança e a segurança da Web 3.
Por um lado, os blockchains buscam cada vez mais escalar além de seus gargalos de rendimento atuais e potencialmente dar suporte à execução, enquanto, por outro, os métodos da Web 2 têm se tornado cada vez mais atacados por proteger inadequadamente os dados e a privacidade do usuário. Como os programadores são capazes de empregar paradigmas de design da Web 3 em seu código da Web 2 e introduzir linguagens e códigos da Web 2 no blockchain, os zk-ASMs genéricos podem representar um ponto de fusão no mundo da Web 2 e da Web 3 [15]. É nesse sentido que o zk-ASM pode nos permitir reimaginar uma Internet mais segura e sem confiança.
🐦 @0xfishylosopher
📅 17 de dezembro de 2022
Aviso Legal: as informações apresentadas acima são puramente educacionais, não constituem aconselhamento financeiro e representam apenas as opiniões do autor. Delphinus Lab é uma empresa de portfólio da Web3.com Ventures.
Referências
[1] https://z.cash/technology/zksnarks/
[2] https://cs251.stanford.edu/lectures/lecture14.pdf
[3] https://www.britannica.com/science/fundamental-theorem-of-algebra
[4] Construindo SNARKs eficientes: https://cs251.stanford.edu/lectures/lecture15.pdf
[5] Exemplo de: https://www.tutorialspoint.com/assembly_programming/assembly_loops.htm
[6] https://en.wikipedia.org/wiki/Assembly_language
[7] https://www.alchemy.com/overviews/zkevm
[8] Para lista de opcodes: https://ethereum.org/en/developers/docs/evm/opcodes/
[9] https://wiki.polygon.technology/docs/zkEVM/zkASM/introduction
[10] https://wiki.polygon.technology/docs/zkEVM/zkASM/some-examples
[11] https://vitalik.ca/general/2022/08/04/zkevm.html
[12] https://blog.developer.adobe.com/understanding-webassembly-wasm-d5b592208ecc
[13] https://jhc.sjtu.edu.cn/~hongfeifu/manuscriptb.pdf
[14] https://hyperoracle.medium.com/zkwasm-the-next-chapter-of-zk-and-zkvm-471038b1fba6
[15] https://delphinuslab.com/zk-wasm/