Jak zk-ASM może zapewnić bezpieczny i pozbawiony zaufania internet
Oryginalna analiza badań Web3.com Ventures
0xFishylosopher
Uwaga: ten artykuł jest dość skomplikowany technicznie i zakłada podstawową znajomość pojęć zk-Proofs i/lub zk-Rollups. Bardziej ogólne wprowadzenie do tych zasad można znaleźć tutaj.

Wstęp
Dowody wiedzy zerowej, w szczególności zk-SNARK (Succinct Non-interactive Arguments of Knowledge), to prawdopodobnie jedna z najważniejszych technologii na pograniczu Web 3. Chociaż większość mediów i uwaga inwestorów w tej dziedzinie skierowana jest w stronę zk -Rollupy, rozwiązania skalujące, które zapewniają skalowalność łańcuchom bloków L1, takim jak Ethereum, nie jest to bynajmniej jedyne zastosowanie zk-SNARK. W tym eseju szczegółowo przeanalizuję koncepcję kodu Zero-Knowledge Assembly (lub zkASM), oceniając jego przypadki użycia zarówno w zk-Rollupach, jak i poza nim, badając jego teoretyczne możliwości w ponownym wynalezieniu Internetu, jaki znamy.
Zasady techniczne
zk-ASM, jak sama nazwa wskazuje, zawiera dwie główne części techniczne: ZK i ASM. Część ZK odnosi się do zk-SNARKs, czyli Succinct Non-Interactive Arguments of Knowledge, podczas gdy część ASM odnosi się do kodu języka assembly. Aby zrozumieć potencjał zk-ASM, musimy najpierw zrozumieć teoretyczne podstawy obu tych pozornie tajemniczych koncepcji.
zk-SNARKs
zk-SNARK to klejnot koronny zk-Dowodów: są zwięzłym dowodem, że pewne stwierdzenie jest Prawdą, gdzie dowód nie ujawnia niczego na temat udowadnianych danych. Na przykład rozważmy kogoś twierdzącego stwierdzenie „Znam m takie, że C(m) = 0”, gdzie m jest wiadomością o długości gigabajta, a C jest funkcją. Zk-SNARK byłby bardzo krótkim dowodem (< 1 GB), który można szybko zweryfikować i w którym nic na temat m nie zostało ujawnione (poza publicznie dostępnymi informacjami) [1].
Czym więc jest to „C(m)”? Jak jest przydatne? Ta funkcja jest w rzeczywistości obwodem arytmetycznym lub reprezentacją ukierunkowanego grafu acyklicznego (DAG) określonej funkcji, którą chcemy wykonać, jak pokazuje diagram [2]. „M” jest zasadniczo danymi wejściowymi do obwodu, a określone „węzły” w obwodzie są indywidualnymi bramkami logicznymi lub operacjami arytmetycznymi. Na przykład węzeł „+” może mieć „2” i „3” jako wejścia i wyprowadzać „5” na następnego operatora. Tak więc dowolna operacja arytmetyczna lub logiczna może być zakodowana w „obwodzie arytmetycznym”.
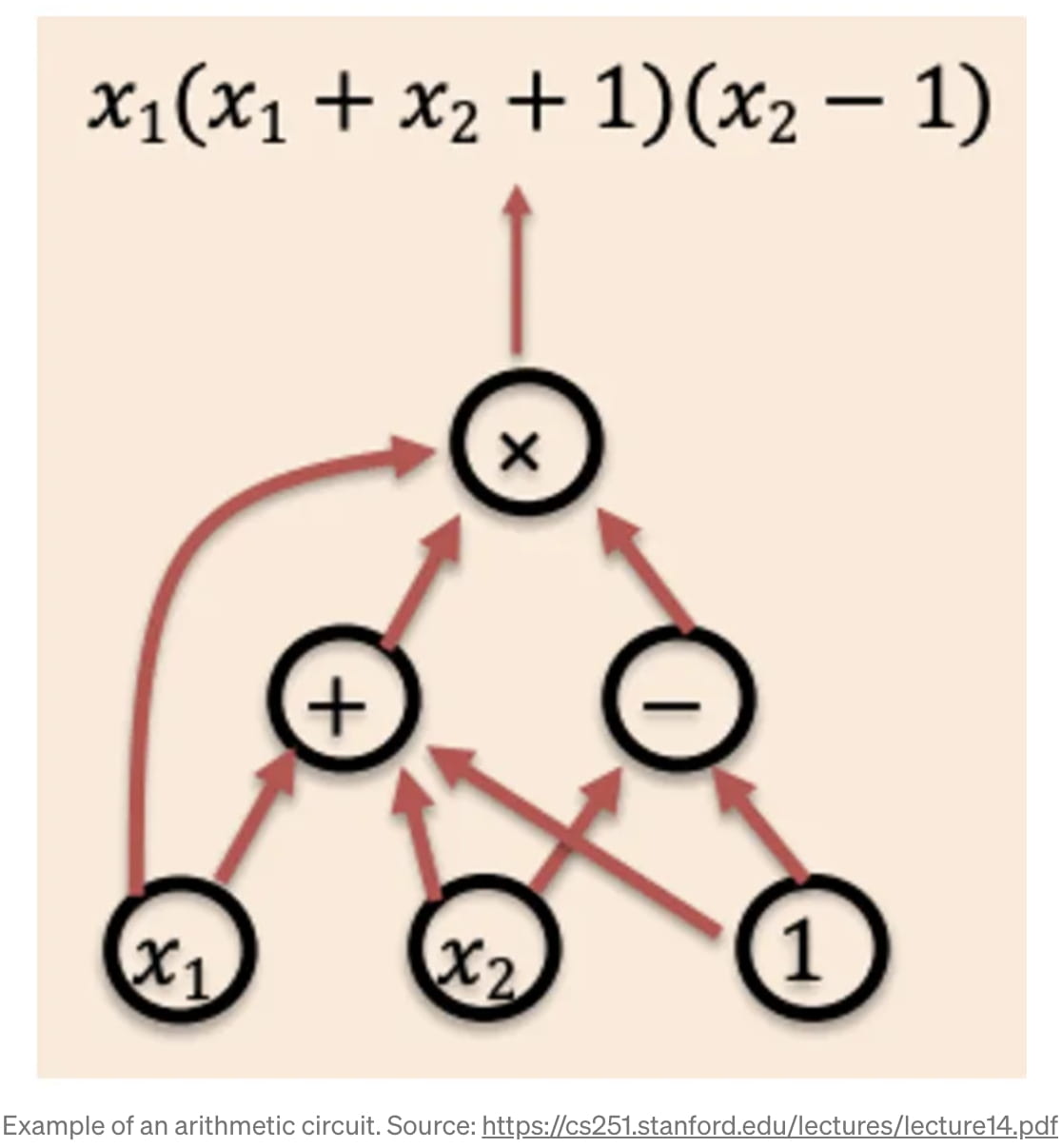
Gdy już mamy ten obwód arytmetyczny jako reprezentację kodu, na którym chcemy uruchomić zk-SNARK, możemy zacząć budować ten zk-SNARK. Zasadniczo zk-SNARK jest możliwy dzięki „podstawowemu twierdzeniu algebry”, które mówi, że wielomian stopnia „d” ma co najwyżej „d” pierwiastków [3]. Matematyczna sztuczka składa się z dwóch kroków: (1) w jakiś sposób przekształcić funkcję „f(m)”, którą chcemy udowodnić, w wielomian (i trzymać się tego) oraz (2) użyć „podstawowego twierdzenia algebry”, aby oddziaływać z wielomianem i dostarczyć zwięzłego dowodu. W żargonie technicznym pierwsza część nazywa się „Polynomial Commitment Scheme” (PCS), a druga część nazywa się „Polynomial Interactive Oracle Proof” (PIOP) [4].
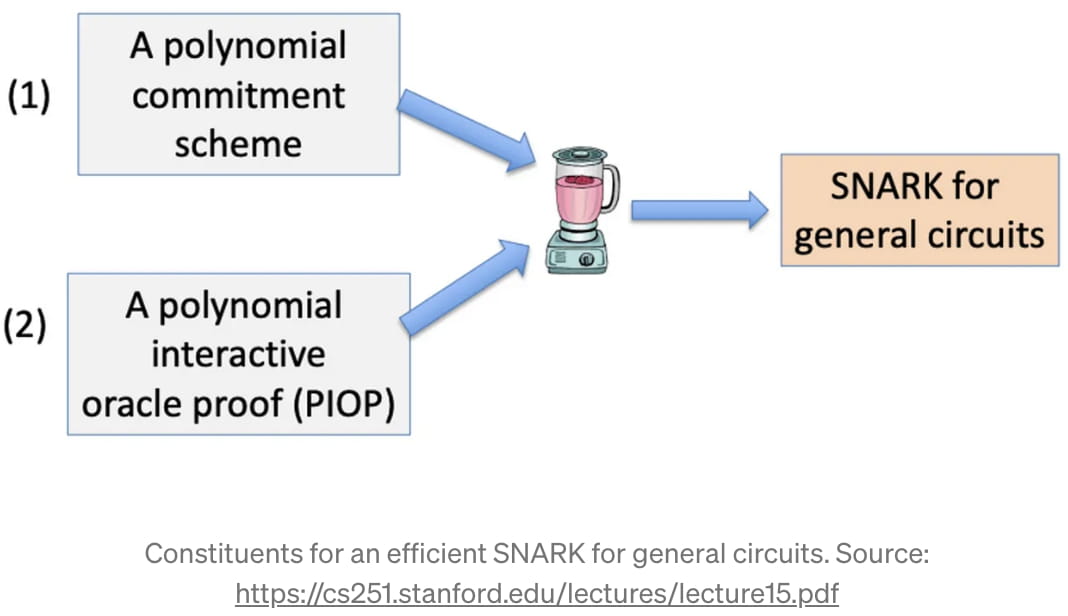
Chociaż szczegółowe implementacje PCS i PIOP wykraczają poza zakres tego artykułu, do tej pory przedstawiliśmy ogólny zarys podstawowych kroków zk-SNARK:
Masz funkcję do wyboru (funkcję kodu, równanie matematyczne itp.), dla której chcesz uruchomić zk-SNARK
Zakoduj tę funkcję jako obwód arytmetyczny C(m)
Uruchom PCS, aby uzyskać wielomianową reprezentację tego obwodu arytmetycznego
Uruchom PIOP, aby uzyskać zwięzły dowód logarytmiczny o rozmiarze do oryginalnego „m”
I viola, mamy specjalnie zaprojektowany zk-SNARK, który może udowodnić, że ktoś zna daną wiadomość, nie ujawniając jej treści.
Kod montażowy
Drugim elementem układanki zk-ASM jest idea kodu asemblera. Kod asemblera to klasa języków zawierających instrukcje napisane w bardzo niskim języku, które są łatwe do odczytania przez maszynę, ale dość trudne do rozszyfrowania przez człowieka. W przeciwieństwie do języków wyższego poziomu, takich jak Python, Java, a nawet C, języki asemblera zawierają bardzo prymitywne funkcje, takie jak przenoszenie, porównywanie, dodawanie i przeskakiwanie w serii rejestrów danych procesora i zakodowanych na stałe lokalizacjach pamięci. Na przykład kod Pythona do drukowania liczb od 1 do 9 na ekranie to 123456789:

Łatwo to zrozumieć, prawda? A oto wersja x86 Assembly [5]:

Znacznie bardziej paskudne, szczególnie w przypadku tak prostej operacji. Więc po co w ogóle używać języka asemblera? Jak wspomniano powyżej, podczas gdy te instrukcje mogą nie być łatwe do odczytania dla człowieka, są bardzo łatwe do „złożenia” w kod bajtowy 110011001, aby maszyna mogła je odczytać i wykonać (to się nazywa asembler) [6]. Porównując, języki wyższego poziomu, takie jak Python i Java, są o wiele bardziej przyjazne dla człowieka, ale programy napisane w tych językach nie mogą być bezpośrednio wykonywane przez procesor. Zamiast tego musimy polegać na „kompilatorze”, który przeżuwa kod Pythona lub Java, który piszemy, i wypluwa zrzut kodu asemblera, taki jak ten powyżej, który jest składany i wykonywany przez maszynę. Możemy oczekiwać, że ten sam fragment Pythona lub Javy będzie działał płynnie na różnych procesorach i różnych systemach operacyjnych, ponieważ kompilator wykonuje ciężką pracę, kompilując kod źródłowy do języka asemblera specyficznego dla danego procesora lub systemu operacyjnego.
Ponieważ wszystkie języki kompilują się do kodu asemblera (który sam jest kompilowany do wykonywalnego pliku binarnego), asembler jest zasadniczo jak „matka wszystkich języków”. Załóżmy teraz, że jesteśmy w stanie przekształcić wszystkie operandy w języku asemblera (takim jak x86 lub RISC-V) w arytmetyczną reprezentację obwodową, tak abyśmy byli w stanie dostarczyć dowody zk-SNARK wszystkich operandów w tym języku asemblera. Oznacza to, że teoretycznie jesteśmy w stanie dostarczyć dowody zk-SNARK dowolnego programu napisanego w dowolnym języku wysokiego poziomu (takim jak Python lub Java), który kompiluje się do tego języka asemblera. I dlatego musimy pomyśleć o zk-ASM-ach.
Zastosowania praktyczne
Zk-EVM Rollups: Wielokąt zk-ASM
Jednym z najważniejszych zastosowań zk-ASM jest tworzenie zgodnych z Ethereum Virtual Machine zk-Rollups, czyli zk-EVM. Zk-EVM jest niezwykle ważny dla skalowalności blockchain, ponieważ pozwala programistom na wdrażanie w łańcuchu L2 opartym na zk-Rollup bez modyfikowania dużej części (jeśli w ogóle) swojego kodu [7]. W tej dziedzinie zk-EVM firmy Polygon jest przykładowym studium przypadku, które pokazuje, jak zk-ASM może być używany do osiągnięcia tego celu.
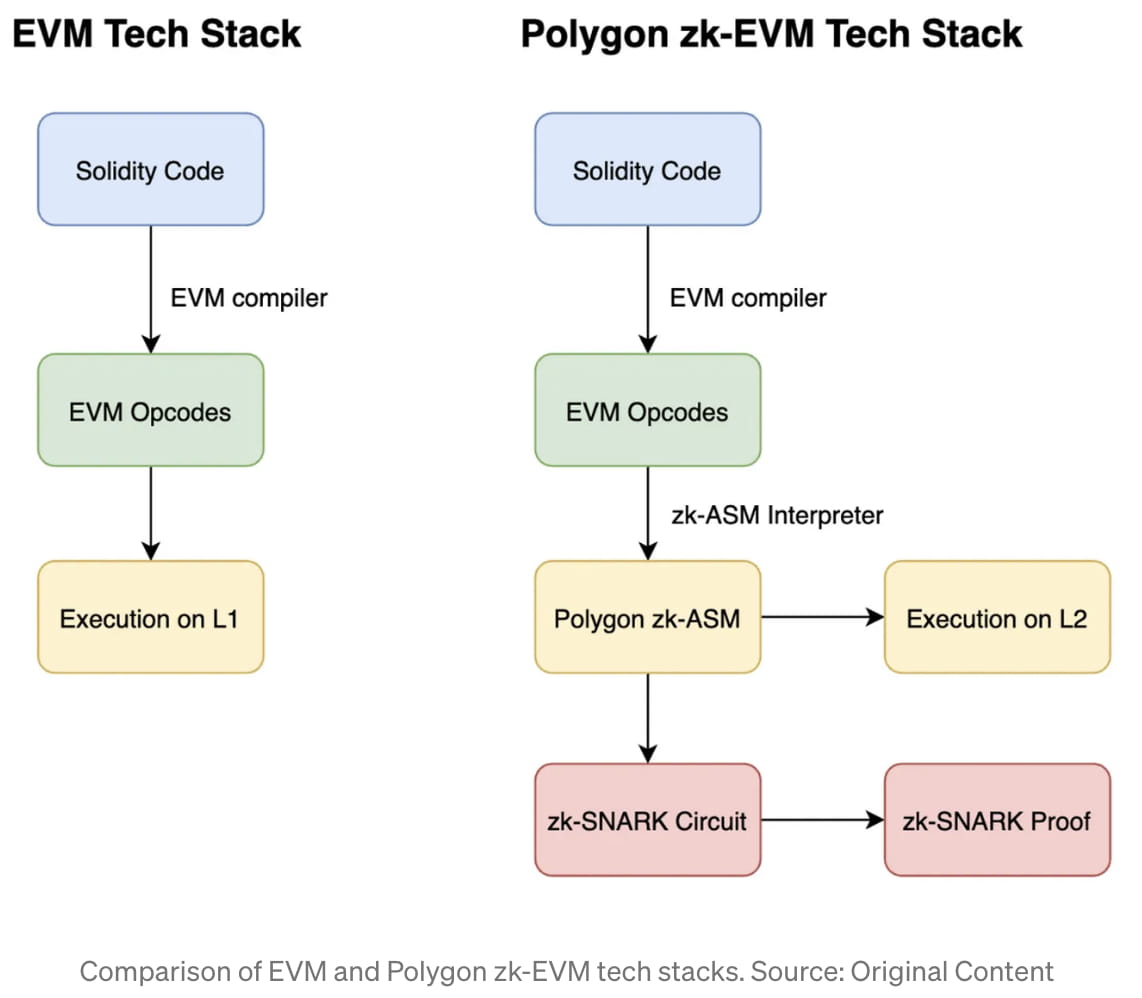
Kiedy programiści tworzą na blockchainie Ethereum L1, zazwyczaj kodują w Solidity, który jest językiem wysokiego poziomu podobnym do C. Ten kod Solidity jest kompilowany do serii kodów operacyjnych EVM, takich jak ADD, SLOAD i EQ, przed wykonaniem na blockchainie L1 [8]. Domyślnie ten proces oczywiście nie tworzy żadnego rodzaju dowodu zk. Sztuczka Polygon polega na stworzeniu metody interpretowania każdego z kodów operacyjnych EVM w ich niestandardowo napisanym zk-ASM, który jest bardzo przyjazny dla zk-SNARK. Następnie ich zk-EVM L2 wykona zk-ASM, jednocześnie tworząc obwód zk-SNARK ASM w celu utworzenia dowodu zk-SNARK [9]. Na przykład kod operacyjny ADD w EVM zostanie przetłumaczony na zk-ASM Polygon w następujący sposób [10]:

Ponieważ sztuczka Polygon zk-EVM ma miejsce na poziomie języka asemblera, jest ona oddalona o dwa poziomy od kodu, którego dotyka przeciętny programista Ethereum, poziomu „Solidity”. To jest powód, dla którego większość programistów może przenieść swój kod EVM stworzony dla głównej sieci Ethereum bezpośrednio do Polygon zk-EVM. Ponadto, ponieważ Polygon zk-EVM „utrzymuje” stos technologiczny Ethereum na poziomie kodu operacji, cała infrastruktura debugowania, która polega na analizowaniu skompilowanych kodów operacji, będzie w pełni użyteczna i nienaruszona. Jest to odmienne od niektórych innych projektów zk-EVM, takich jak zk-Sync, który nie zapewnia dowodów zk na poziomie kodu operacji. Tak więc, nawet gdy Polygon wymyśla i udowadnia swój własny język asemblera, Vitalik pisze, że „nadal może weryfikować kod EVM, po prostu używa do tego innej wewnętrznej logiki” [11].
Poza Rollupami: zk-WASM
zk-EVM nie są bynajmniej jedynym zastosowaniem zk-ASM. Przypomnijmy nasze poprzednie stwierdzenie, że języki asemblera są zasadniczo „matką wszystkich języków” i że stworzenie zk-ASM odblokuje dowody zk dla programów generycznych napisanych w dowolnym języku, który kompiluje się do tego języka asemblera. Web Assembly, lub WASM, jest jednym z najważniejszych powstających języków asemblera. Po raz pierwszy opublikowany w 2018 r., WASM ma na celu stworzenie języka asemblera, który zwiększyłby szybkość wykonywania aplikacji internetowych i zapewnił uzupełnienie wykonawcze dla Javascript, podstawowego języka kodowania w sieci [12].
Zasadniczo, wraz z rozwojem sieci Web na przestrzeni lat, rosnący rozmiar i złożoność aplikacji internetowych oznaczały, że często przeglądarkom jest niezwykle wolno kompilować wszystko, co zostało napisane w Javascript, i muszą polegać na złożonych cyklach kompilacji-optymalizacji-ponownego ładowania [12]. Z drugiej strony WebAssembly eliminuje potrzebę polegania na złożonych silnikach wykonawczych przeglądarki, zapewniając przenośny, modułowy i łatwo wykonywalny język asemblera. Ponadto, jako język asemblera, WASM pozwala programistom na bezpośrednie pisanie fragmentów kodu w C, C++, Rust, Java lub Ruby, które działają natywnie w przeglądarce. WASM stał się zatem technologią z wyboru w celu „zapewnienia rozproszonych funkcji bezserwerowych” [13].
Dlaczego więc i w jaki sposób zk-SNARKs wchodzą w grę? WASM jest wyjątkowy, ponieważ jest technologią po stronie klienta, zdolną do bezpośredniej interakcji z danymi wejściowymi i danymi użytkownika. Ponieważ często obejmuje to poufne dane, takie jak hasła i informacje osobiste, potrzebujemy technologii, która (1) zapewnia, że program wykonuje się poprawnie i że (2) nasze poufne informacje nie wyciekają. Jak opisano powyżej, zk-SNARK jest idealnym rozwiązaniem do rozwiązania obu tych problemów i jest zatem ważnym elementem układanki w zabezpieczaniu WASM [14].
Podczas gdy prace nad rozwojem zk-WASM są wciąż na wczesnym etapie, ostatnio pojawiło się kilka projektów, które wydały prototypowe obwody zk-SNARK dla WebAssembly. Na przykład emulator zk-SNARK „ZAWA” Delphinus Lab prezentuje metodę kodowania operandów i semantyki maszyny wirtualnej WASM w obwodzie arytmetycznym, co pozwala jej na przeprowadzanie dowodów zk-SNARK [13]. W miarę upływu czasu obwody zk-WASM będą niewątpliwie stale optymalizowane, co pozwoli programom napisanym w językach generycznych (takich jak C, C++, Rust i Ruby) na przyjęcie paradygmatu dowodów zk.
Wniosek
W tym eseju zbadaliśmy teoretyczne podstawy zk-ASM, a także przeanalizowaliśmy dwa paradygmatyczne studia przypadków zk-ASM: użycie zk-ASM przez Polygon do stworzenia zk-EVM na poziomie kodu operacji, a także zastosowanie zk-SNARKs w WebAssembly do stworzenia zk-WASM. Ostatecznie obietnicą zk-ASM jest połączenie interoperacyjności i skali Web 2 z brakiem zaufania i bezpieczeństwem Web 3.
Z jednej strony blockchainy coraz częściej starają się skalować poza swoje obecne wąskie gardła przepustowości i potencjalnie wspierać wykonanie, podczas gdy z drugiej strony metody Web 2 są coraz częściej atakowane za niewystarczającą ochronę danych użytkowników i prywatności. Ponieważ programiści są w stanie stosować paradygmaty projektowania Web 3 w swoim kodzie Web 2 i wprowadzać języki i kod Web 2 do blockchain, generyczne zk-ASM mogą stanowić punkt połączenia w świecie Web 2 i Web 3 [15]. W tym sensie zk-ASM może pozwolić nam na ponowne wyobrażenie sobie bezpieczniejszego i pozbawionego zaufania Internetu.
🐦 @0xfishylosopher
📅 17 grudnia 2022
Zastrzeżenie: informacje przedstawione powyżej mają charakter wyłącznie edukacyjny, nie stanowią porady finansowej i reprezentują wyłącznie poglądy autora. Delphinus Lab jest spółką portfelową Web3.com Ventures.
Odniesienia
[1] https://z.cash/technology/zksnarks/
[2] https://cs251.stanford.edu/lectures/lecture14.pdf
[3] https://www.britannica.com/science/fundamental-theorem-of-algebra
[4] Tworzenie wydajnych SNARK-ów: https://cs251.stanford.edu/lectures/lecture15.pdf
[5] Przykład z: https://www.tutorialspoint.com/assembly_programming/assembly_loops.htm
[6] https://en.wikipedia.org/wiki/Assembly_language
[7] https://www.alchemy.com/overviews/zkevm
[8] Lista kodów operacji: https://ethereum.org/en/developers/docs/evm/opcodes/
[9] https://wiki.polygon.technology/docs/zkEVM/zkASM/introduction
[10] https://wiki.polygon.technology/docs/zkEVM/zkASM/some-examples
[11] https://vitalik.ca/general/2022/08/04/zkevm.html
[12] https://blog.developer.adobe.com/understanding-webassembly-wasm-d5b592208ecc
[13] https://jhc.sjtu.edu.cn/~hongfeifu/manuscriptb.pdf
[14] https://hyperoracle.medium.com/zkwasm-the-next-chapter-of-zk-and-zkvm-471038b1fba6
[15] https://delphinuslab.com/zk-wasm/