Comment zk-ASM peut fournir un Internet sécurisé et sans confiance
Analyse de recherche originale de Web3.com Ventures
0xPoissonlosophe
Remarque : Cet article est un article assez dense sur le plan technique et suppose une familiarité conceptuelle de base avec zk-Proofs et/ou zk-Rollups. Une introduction plus générale à ces principes peut être trouvée ici.

Introduction
Les Zero Knowledge Proofs, en particulier les zk-SNARK (Succinct Non-interactive Arguments of Knowledge) sont peut-être l'une des technologies les plus importantes aux frontières du Web 3. Alors que la majeure partie de l'attention des médias et des investissements dans ce sous-domaine s'est tournée vers zk -Rollups, solutions de mise à l'échelle qui offrent une grande évolutivité aux blockchains L1 telles que Ethereum, ce n'est en aucun cas la seule application des zk-SNARK. Dans cet essai, j'analyserai en profondeur le concept de code Zero-Knowledge Assembly (ou zkASM), en évaluant ses cas d'utilisation dans zk-Rollups et au-delà, en explorant ses possibilités théoriques pour réinventer l'Internet tel que nous le connaissons.
Principes techniques
zk-ASM, comme son nom l'indique, contient deux parties techniques principales : ZK et ASM. La partie ZK fait référence aux zk-SNARK, ou arguments succincts non interactifs de connaissances, tandis que la partie ASM fait référence au code Assembly. Pour comprendre le potentiel de zk-ASM, nous devons d’abord comprendre les fondements théoriques de ces deux concepts apparemment obscurs.
zk-SNARK
Les zk-SNARK sont les joyaux de zk-Proofs : ils sont une preuve succincte qu'une certaine déclaration est vraie où la preuve ne révèle rien sur les données à prouver. Par exemple, considérons quelqu'un affirmant la déclaration « Je connais un m tel que C(m) = 0 », où m est un message d'un gigaoctet et C est une fonction. Un zk-SNARK serait une preuve très courte (< 1 Go) qui peut être rapidement vérifiée et dans laquelle rien sur m n'est révélé (au-delà des informations accessibles au public) [1].
Alors, quel est ce « C(m) » ? En quoi est-ce utile ? Cette fonction est en fait un circuit arithmétique, ou une représentation graphique acyclique dirigée (DAG) d'une fonction spécifique que nous voulons exécuter, comme le montre le diagramme [2]. Le « m » correspond essentiellement aux données d'entrée dans le circuit, et les « nœuds » spécifiques du circuit sont des portes logiques individuelles ou des opérations arithmétiques. Par exemple, un nœud « + » peut avoir « 2 » et « 3 » comme entrées et afficher un « 5 » sur l'opérateur suivant. Ainsi, une opération arithmétique ou logique arbitraire peut être codée dans un « circuit arithmétique ».
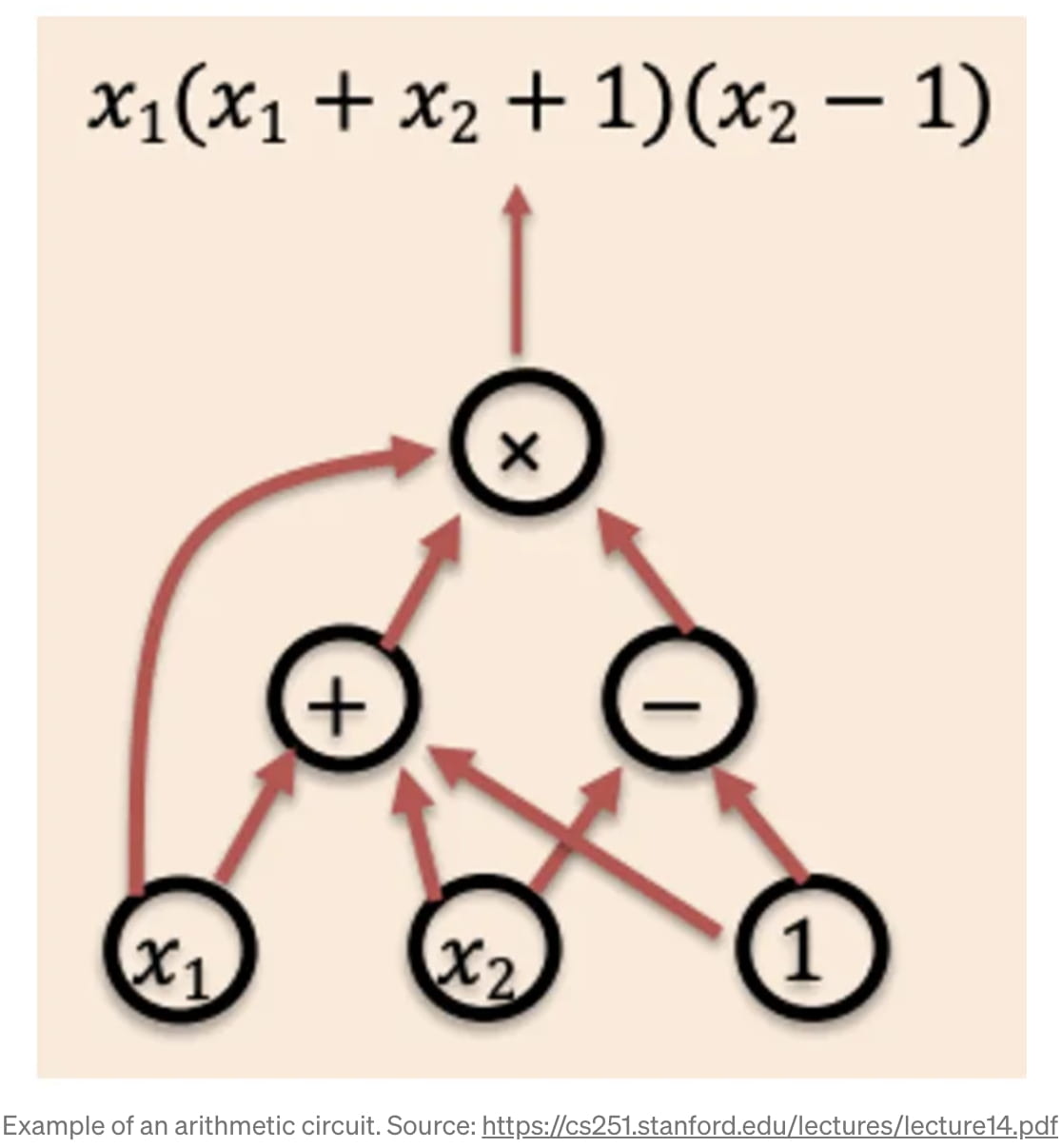
Une fois que nous avons ce circuit arithmétique comme représentation du code sur lequel nous voulons exécuter un zk-SNARK, nous pouvons commencer à construire ce zk-SNARK. Fondamentalement, un zk-SNARK est possible grâce au « théorème fondamental de l'algèbre », qui stipule qu'un polynôme de degré « d » a au plus des racines « d » [3]. L'astuce mathématique comporte deux étapes : (1) convertir d'une manière ou d'une autre la fonction "f(m)" que nous voulons prouver en un polynôme (et s'en tenir à cela), et (2) utiliser le "théorème fondamental de l'algèbre" pour interagir avec le polynôme et fournir une preuve succincte. Dans le jargon technique, la première partie est appelée « Polynomial Commitment Scheme » (PCS), et la deuxième partie est appelée « Polynomial Interactive Oracle Proof » (PIOP) [4].
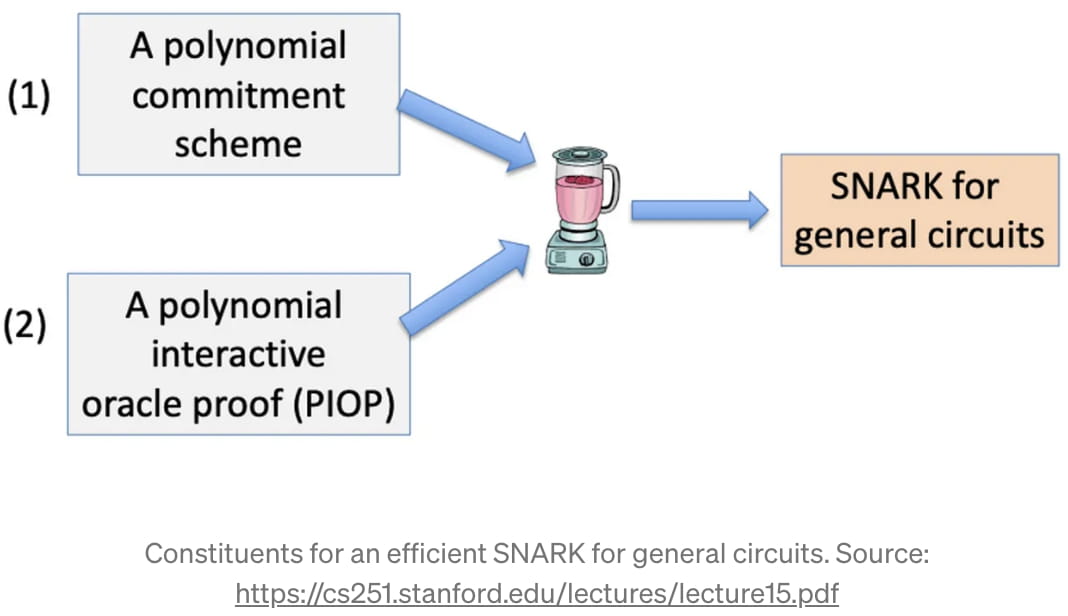
Bien que les implémentations spécifiques d'un PCS et d'un PIOP dépassent le cadre de cet article, nous avons jusqu'à présent dressé une esquisse des étapes principales d'un zk-SNARK :
Avoir une fonction de choix (fonction de code, équation mathématique, etc.) avec laquelle vous souhaitez exécuter un zk-SNARK
Coder cette fonction sous forme de circuit arithmétique C(m)
Exécutez un PCS pour obtenir une représentation polynomiale de ce circuit arithmétique
Exécutez un PIOP pour obtenir une preuve succincte de la taille logarithmique au « m » d'origine
Et voilà, nous avons un zk-SNARK personnalisé qui peut prouver que quelqu'un connaît un message donné sans révéler quel est ce message.
Code d'assemblage
La deuxième pièce du puzzle de zk-ASM est l'idée du code d'assemblage. Le code assembleur est une classe de langages contenant des instructions en langage très simple, faciles à lire pour une machine mais assez difficiles à déchiffrer pour un humain. Contrairement aux langages de niveau supérieur, tels que Python, Java ou même C, les langages Assembly contiennent des fonctions très primitives, telles que déplacer, comparer, ajouter et sauter sur une série de registres de données sur le processeur et des emplacements de mémoire codés en dur. Par exemple, le code Python permettant d'imprimer les chiffres de 1 à 9 à l'écran est 123456789 :

Assez facile à comprendre, non ? En voici maintenant la version x86 Assembly [5] :

Beaucoup plus méchant, surtout pour une opération aussi simple. Alors pourquoi même utiliser le langage Assembly ? Comme indiqué ci-dessus, même si ces instructions ne sont pas faciles à lire pour un humain, elles sont très faciles à « assembler » dans le code 1 10011001 octets pour qu'une machine puisse les lire et les exécuter (c'est ce qu'on appelle un assembleur) [6]. Comparativement parlant, les langages de niveau supérieur tels que Python et Java sont beaucoup plus conviviaux à lire, mais les programmes écrits dans ces langages ne peuvent pas être directement exécutés par un processeur. Au lieu de cela, nous devons nous appuyer sur un « compilateur » qui mâche le code Python ou Java que nous écrivons et crache un dump de code assembleur comme celui ci-dessus pour être assemblé et exécuté par la machine. Nous pouvons nous attendre à ce que le même morceau de Python ou Java fonctionne correctement sur différents processeurs et différents systèmes d'exploitation, car le compilateur fait le gros du travail, en compilant votre code source dans un langage Assembly spécifique à ce processeur ou à ce système d'exploitation.
Étant donné que tous les langages se compilent en code assembleur (qui lui-même est compilé en binaire exécutable), l'assembleur est essentiellement comme la « mère de tous les langages ». Supposons maintenant que nous soyons capables de transformer tous les opérandes d'un langage Assembly (tel que x86 ou RISC-V) en une représentation de circuit arithmétique, de telle sorte que nous puissions fournir des preuves zk-SNARK de tous les opérandes de cet Assembly. langue. Cela signifie que nous sommes théoriquement capables de fournir un zk-SNARK de tout programme écrit dans un langage arbitraire de haut niveau (tel que Python ou Java) qui se compile dans ce langage Assembly. Et c’est pourquoi nous devons réfléchir aux zk-ASM.
Applications pratiques
Cumuls zk-EVM : Polygone zk-ASM
L'une des applications les plus importantes de zk-ASM consiste à créer des zk-Rollups, ou zk-EVM, compatibles avec la machine virtuelle Ethereum. Un zk-EVM est extrêmement important pour l'évolutivité de la blockchain car il permet aux programmeurs de se déployer sur une chaîne L2 basée sur zk-Rollup sans modifier beaucoup (le cas échéant) de leur code [7]. Dans ce domaine, le zk-EVM de Polygon est une étude de cas exemplaire qui démontre comment zk-ASM peut être utilisé pour atteindre cet objectif.
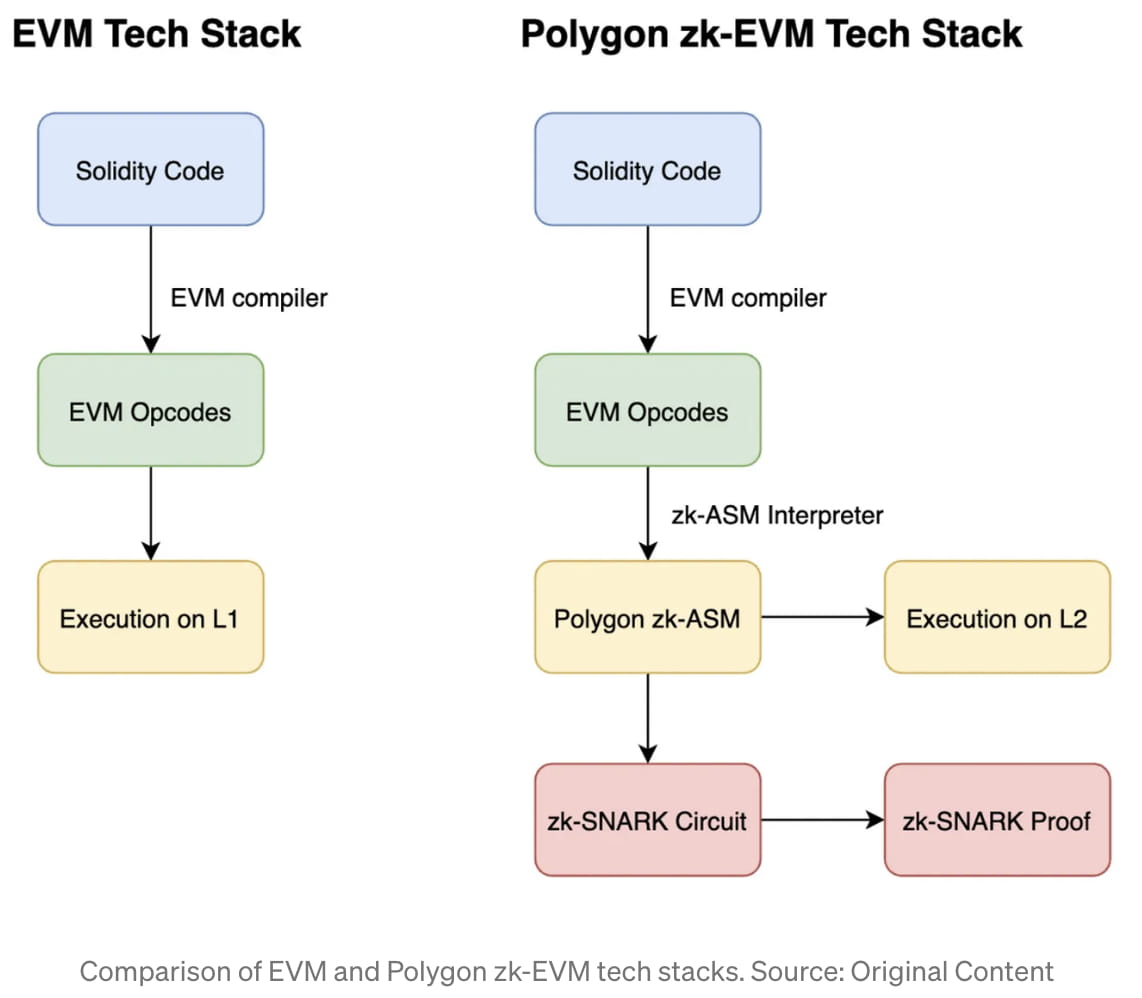
Lorsque les programmeurs développent sur la blockchain Ethereum L1, ils codent généralement en Solidity, qui est un langage de haut niveau proche du C. Ce code Solidity est compilé en une série d'opcodes EVM, tels que ADD, SLOAD et EQ, avant d'être exécuté. sur la blockchain L1 [8]. Par défaut, ce processus ne crée évidemment aucune sorte de zk-Proof. L'astuce de Polygon consiste à créer une méthode pour interpréter chacun des opcodes EVM dans leur zk-ASM écrit sur mesure, qui est très convivial pour zk-SNARK. Ensuite, leur L2 zk-EVM exécutera le zk-ASM, tout en créant également un circuit zk-SNARK de l'ASM afin de créer une preuve zk-SNARK [9]. Par exemple, l'opcode ADD dans l'EVM sera traduit en zk-ASM de Polygon comme suit [10] :

Étant donné que le tour de passe-passe de Polygon zk-EVM se produit au niveau de l'assemblage, ce sont deux niveaux éloignés du code que le programmeur Ethereum moyen touche, le niveau « Solidité ». C'est la raison pour laquelle la plupart des développeurs peuvent porter leur code EVM créé pour le réseau principal Ethereum directement sur Polygon zk-EVM. De plus, étant donné que Polygon zk-EVM « maintient » la pile technologique d'Ethereum jusqu'au niveau des opcodes, toute l'infrastructure de débogage qui repose sur l'analyse des opcodes compilés restera utilisable et intacte. Ceci est différent de certaines autres conceptions zk-EVM, telles que zk-Sync, qui ne fournissent pas de zk-Proofs au niveau de l'opcode. Ainsi, même si Polygon invente et prouve son propre langage Assembly, Vitalik écrit qu '«il peut toujours vérifier le code EVM, il utilise simplement une logique interne différente pour le faire» [11].
Au-delà des cumuls : zk-WASM
Les zk-EVM ne sont en aucun cas la seule application pour les zk-ASM. Rappelez-vous notre affirmation précédente selon laquelle les langages Assembly sont essentiellement « la mère de tous les langages » et que la création d'un zk-ASM débloquera des zk-Proofs pour les programmes génériques écrits dans n'importe quel langage compilé dans ce langage Assembly. Web Assembly, ou WASM, est l'un des langages d'assemblage émergents les plus importants. Publié pour la première fois en 2018, le but de WASM est de créer un langage Assembly qui augmente la vitesse d'exécution des applications Web et fournit un complément d'exécution à Javascript, le principal langage de codage derrière le Web [12].
Essentiellement, à mesure que le Web se développait au fil des années, la taille et la complexité croissantes des applications Web signifiaient qu'il était souvent incroyablement lent pour les navigateurs de compiler tout ce qui était écrit en Javascript et qu'il devait s'appuyer sur des cycles complexes de compilation, d'optimisation et de rechargement [12]. WebAssembly, d'autre part, supprime le besoin de s'appuyer sur des moteurs d'exécution de navigateur complexes en fournissant un langage d'assemblage portable, modulaire et facilement exécutable. De plus, en tant que langage Assembly, WASM permet aux programmeurs d'écrire directement des extraits de code en C, C++, Rust, Java ou Ruby qui s'exécutent nativement dans un navigateur. WASM est donc devenu une technologie de choix pour « fournir des fonctions distribuées sans serveur » [13].
Alors pourquoi et comment les zk-SNARK entrent-ils en scène ? WASM est unique en ce sens qu'il s'agit d'une technologie côté client, capable d'interagir directement avec les entrées et les données de l'utilisateur. Étant donné que cela inclut souvent des données sensibles telles que des mots de passe et des informations personnelles, nous avons besoin d'une technologie qui (1) garantit que le programme s'exécute correctement et que (2) nos informations sensibles ne sont pas divulguées. Comme décrit ci-dessus, un zk-SNARK est une solution parfaite pour résoudre ces deux problèmes et constitue donc une pièce importante du puzzle dans la sécurisation de WASM [14].
Bien que les travaux de développement de zk-WASM en soient encore à leurs débuts, certains projets ont récemment publié des prototypes de circuits zk-SNARK pour WebAssembly. Par exemple, l'émulateur zk-SNARK « ZAWA » de Delphinus Lab présente une méthode pour coder les opérandes et la sémantique d'une machine virtuelle WASM dans un circuit arithmétique, ce qui lui permet d'effectuer des preuves zk-SNARK [13]. Au fil du temps, les circuits zk-WASM seront sans aucun doute continuellement optimisés, permettant ainsi aux programmes écrits dans des langages génériques (tels que C, C++, Rust et Ruby) d'adopter le paradigme des zk-Proofs.
Conclusion
Tout au long de cet essai, nous avons exploré les fondements théoriques de zk-ASM ainsi que deux études de cas paradigmatiques de zk-ASM : l'utilisation par Polygon de zk-ASM pour créer un zk-EVM au niveau de l'opcode, ainsi que l'application de zk. -SNARKs sur WebAssembly pour créer zk-WASM. En fin de compte, la promesse de zk-ASM est de combiner l'interopérabilité et l'évolutivité du Web 2 avec le manque de confiance et la sécurité du Web 3.
D'une part, les chaînes de blocs cherchent de plus en plus à dépasser leurs goulots d'étranglement actuels en matière de débit et à potentiellement prendre en charge l'exécution, tandis que d'autre part, les méthodes Web 2 sont de plus en plus attaquées pour leur protection insuffisante des données et de la vie privée des utilisateurs. Étant donné que les programmeurs sont capables d'utiliser les paradigmes de conception Web 3 dans leur code Web 2 et d'introduire les langages et le code Web 2 dans la blockchain, les zk-ASM génériques peuvent représenter un point de fusion dans le monde du Web 2 et du Web 3 [15]. C’est dans ce sens que zk-ASM peut nous permettre de réinventer un Internet plus sécurisé et sans confiance.
🐦 @0xfishylosopher
📅 17 décembre 2022
Avertissement : les informations présentées ci-dessus sont purement éducatives, ne constituent pas des conseils financiers et représentent uniquement le point de vue de l'auteur. Delphinus Lab est une société de portefeuille de Web3.com Ventures.
Les références
[1] https://z.cash/technology/zksnarks/
[2] https://cs251.stanford.edu/lectures/lecture14.pdf
[3] https://www.britannica.com/science/fundamental-theorem-of-algebra
[4] Créer des SNARK efficaces : https://cs251.stanford.edu/lectures/lecture15.pdf
[5] Exemple tiré de : https://www.tutorialspoint.com/assembly_programming/assembly_loops.htm
[6] https://en.wikipedia.org/wiki/Assembly_langue
[7] https://www.alchemy.com/overviews/zkevm
[8] Pour la liste des opcodes : https://ethereum.org/en/developers/docs/evm/opcodes/
[9] https://wiki.polygon.technology/docs/zkEVM/zkASM/introduction
[10] https://wiki.polygon.technology/docs/zkEVM/zkASM/some-examples
[11] https://vitalik.ca/general/2022/08/04/zkevm.html
[12] https://blog.developer.adobe.com/understanding-webassembly-wasm-d5b592208ecc
[13] https://jhc.sjtu.edu.cn/~hongfeifu/manuscriptb.pdf
[14] https://hyperoracle.medium.com/zkwasm-the-next-chapter-of-zk-and-zkvm-471038b1fba6
[15] https://delphinuslab.com/zk-wasm/