In der modernen Finanztheorie geht die Bewertung der Investmentperformance oft über die traditionelle Analyse der durchschnittlichen Rendite und der Standardabweichung hinaus. Während etablierte Kennzahlen wie das Sharpe-Verhältnis von der Annahme einer Normalverteilung der Renditen ausgehen, zeigen die realen Marktdaten – insbesondere für digitale Vermögenswerte wie Bitcoin (BTC) – häufig Asymmetrie und "fette Schwänze". Das Omega-Verhältnis bietet einen grundlegend anderen Ansatz, indem es die gesamte kumulierte Verteilung der Renditen nutzt, um das Gewinnpotenzial vom Verlustrisiko im Verhältnis zu einem definierten Schwellenwert zu unterscheiden.
1. Definition und mathematische Grundlage
Laut der Forschung von Kapsos et al. (2011) ermöglicht das Omega-Verhältnis Analysten, die Wahrscheinlichkeit zu bewerten, eine bestimmte Zielrendite zu erreichen, indem sie die gesamte Wahrscheinlichkeitsdichte integrieren. Das Verhältnis wird definiert als das Verhältnis zwischen wahrscheinlichkeitssensitiven Gewinnen und wahrscheinlichkeitssensitiven Verlusten bei einer Mindestakzeptablen Rendite (MAR) Schwelle.
Die mathematische Darstellung von Omega (Ω) wird über die kumulative Verteilungsfunktion (CDF) abgeleitet:
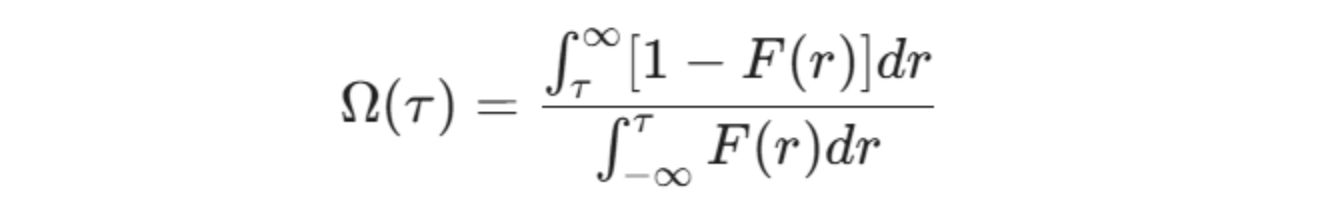
Wo:
Ω: Das Omega-Verhältnis.
𝞃 (tau): Die von dem Investor definierte Mindestakzeptable Rendite (MAR) Schwelle.
F(r): Die kumulative Verteilungsfunktion (CDF) der Renditen des Assets.
r: Die Rendite des Assets.
Durch partielle Integration kann die Gleichung in einer rechnerisch anwendbaren Form basierend auf den erwarteten Werten dargestellt werden. Dies bestimmt die Masse der Rückverteilung über der Schwelle [𝞃, +∞] (positive Rendite relativ zu 𝞃) und unterhalb der Schwelle [-∞, 𝞃] (negative Rendite relativ zu 𝞃):
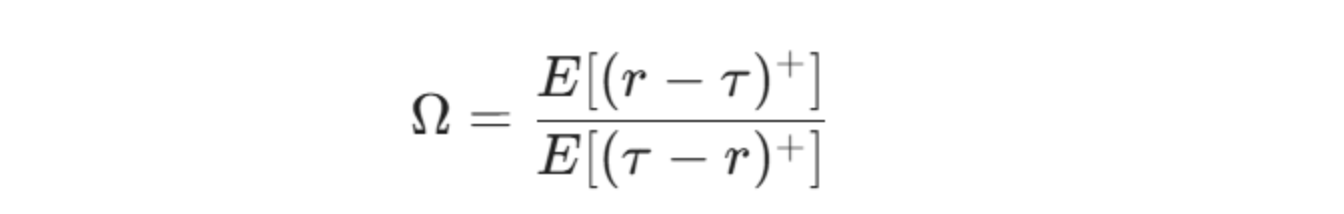
Wo:
E[(r - 𝞃)+]: Der erwartete Wert der Gewinne über der Schwelle 𝞃.
E[(𝞃 - r)+]: Der erwartete Wert der Verluste unter der Schwelle 𝞃.
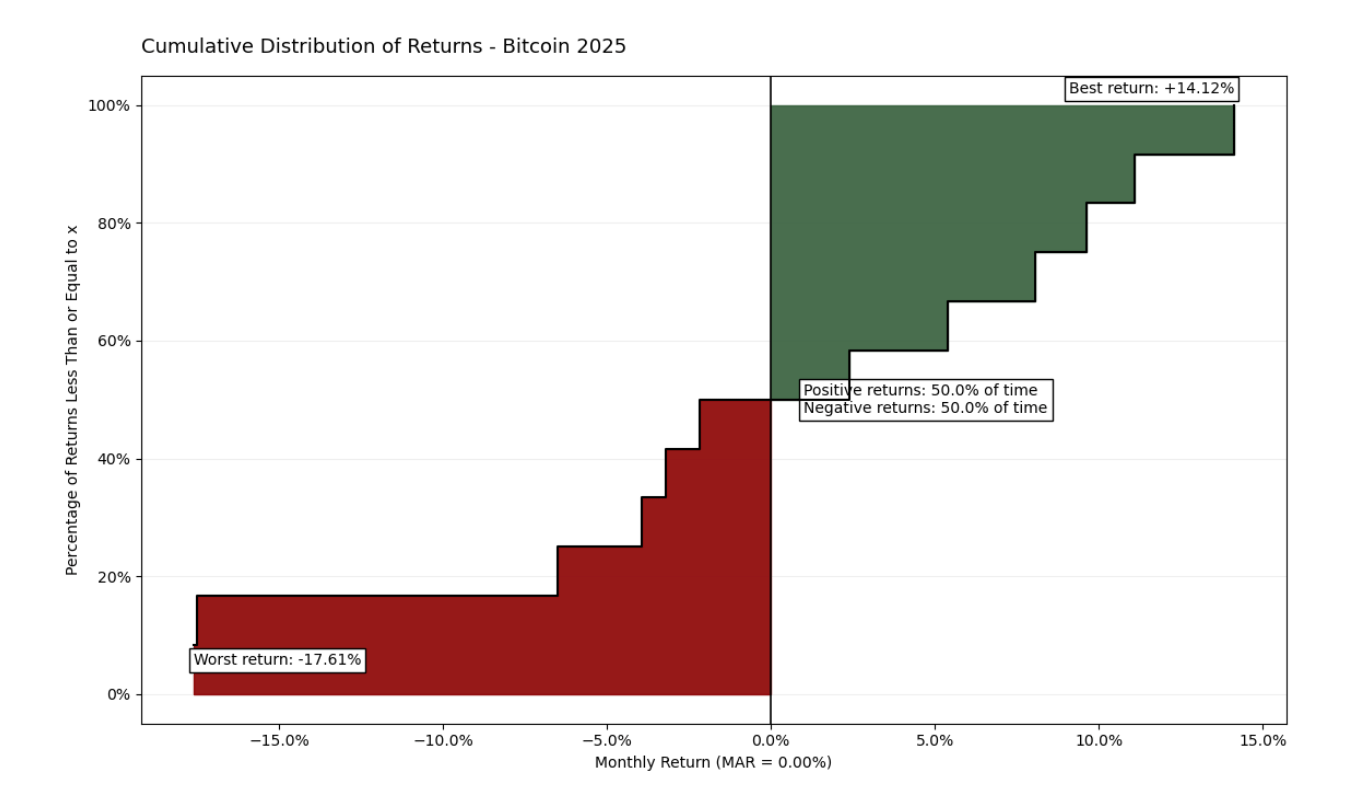
Die Daten von 2025 veranschaulichen die asymmetrische Volatilität des Assets, mit extremen Schwankungen zwischen -17,61 % und +14,12 %. Trotz einer ausgewogenen Frequenz (50 % positive vs. 50 % negative Monate) offenbart ein Omega-Verhältnis von 0,778 ein höheres Gewicht der Verluste im linken Ende der Kurve. Diese visuelle Parität betont, dass die Größe der Rückgänge die Rallyes dominiert und eine grundlegende Basis für die Bewertung der Asset-Qualität im Verhältnis zum gewählten MAR darstellt.
Während ein einjähriges Diagramm sperrig und weniger informativ erscheinen mag, bietet die Erweiterung des Zeitrahmens auf einen Zeitraum von 10 Jahren ein signifikant umfassenderes Bild.
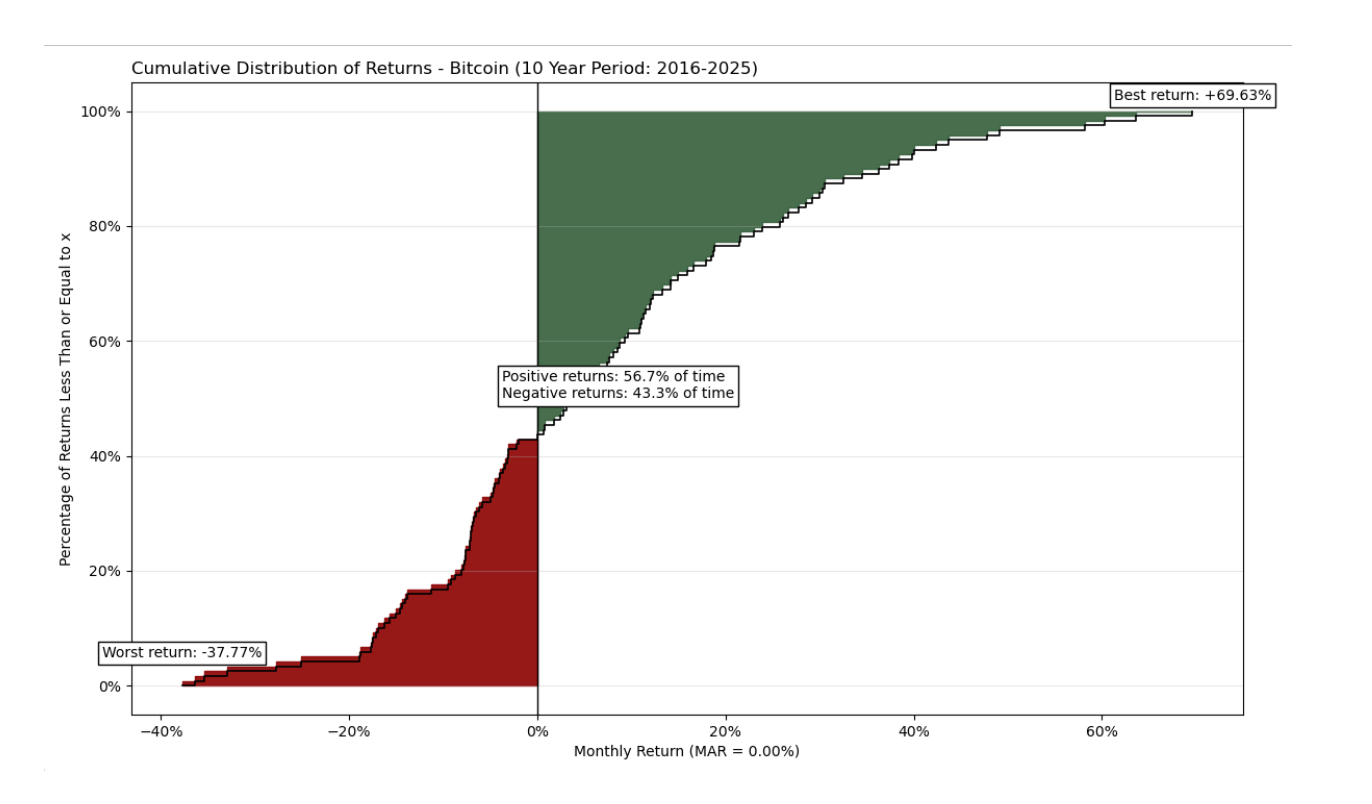
Die 10-Jahres-Analyse zeigt ein viel günstigeres Risiko-Rendite-Profil. Obwohl das Asset extreme Volatilität mit monatlichen Rückgängen von bis zu -37,77 % beibehält, zeigt es ein beeindruckendes Wachstumspotenzial mit Spitzen von bis zu +69,63 %. Im Gegensatz zur einjährigen Momentaufnahme dominieren hier die positiven Monate (56,7 % der Zeit), und die "grüne Zone" des Gewinns überwiegt visuell und mathematisch die "rote Zone" des Risikos. Das Omega-Verhältnis für diesen Zeitraum beträgt 1,621, was beweist, dass Bitcoin eine signifikante Prämie im Verhältnis zum eingegangenen Risiko über einen längeren Zeitraum generiert.
2. Interpretation und Risikoanalyse
Im Gegensatz zu anderen Koeffizienten hängt der Wert von Omega direkt von der gewählten Schwelle 𝞃 ab. Dies macht die Metrik anpassungsfähig an das spezifische Risiko-Profil des Anlegers.
Ω > 1: Zeigt an, dass der kumulierte Wert der Gewinne den der Verluste relativ zur gewählten MAR übersteigt. Eine höhere Zahl bedeutet eine bessere Qualität der Renditen.
Ω = 1: Bedeutet, dass die erwartete Rendite des Assets genau der Schwelle 𝞃 entspricht.
Ω < 1: Signalisiert, dass das Risiko eines Verlusts unterhalb der gewählten "Barriere" die potenzielle Gewinnchance überwiegt.
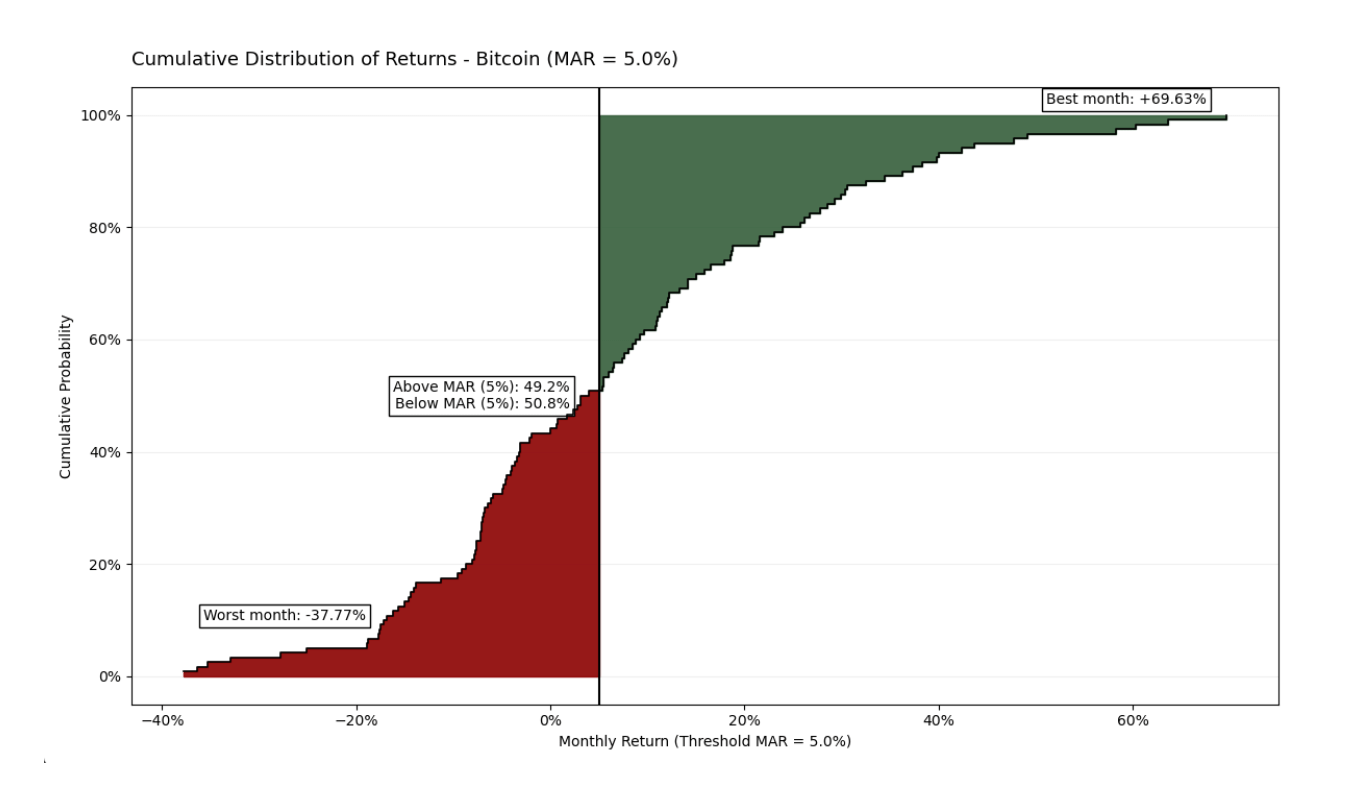
Im analysierten 10-Jahres-Zeitraum platziert die Anwendung eines MAR von 5 % monatlich das Asset in einem strengeren Rahmen. Obwohl Bitcoin in diesem Zeitraum 50,8 % der Zeit unterhalb dieser Schwelle bleibt, bleibt sein Omega-Verhältnis mit 1,2102 positiv. Dies bestätigt, dass der Beitrag "explosiver" Monate (die bis zu +69,63 % erreichen) stark genug ist, um den kumulativen Effekt von Monaten mit negativen oder mittelmäßigen Renditen zu überwiegen. Die Daten beweisen, dass Bitcoin selbst bei hohen Investitionserwartungen seinen statistischen Vorteil auf lange Sicht beibehält.
3. Optimierung durch lineare Programmierung
Eine der bedeutendsten praktischen Anwendungen des Omega-Verhältnisses, die von Kapsos et al. (2011) detailliert beschrieben wird, ist seine Verwendung im aktiven Portfolioaufbau. Während die Funktion zunächst komplex erscheinen mag, beweisen die Autoren, dass die Maximierung von Omega als Problem der linearen Programmierung umformuliert werden kann.
Der diskrete Analog von Omega für rechnerische Zwecke über $m$ historische Beobachtungen ist:
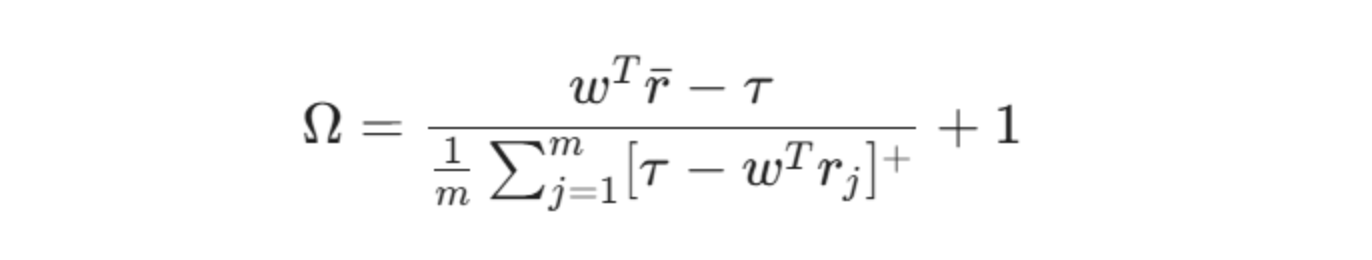
Wo:
𝑤: Vektor der Asset-Gewichte im Portfolio.
r: Vektor der durchschnittlichen historischen Renditen.
m: Anzahl der historischen Beobachtungen (Stichproben).
rj: Vektor der Renditen für jede spezifische Beobachtung ⅉ.
Dieser Ansatz unterscheidet sich grundlegend von der traditionellen Markowitz- (Mean-Variance) Optimierung. Anstatt einfach die Volatilität zu minimieren (die schnelle Aufwärtsbewegungen bestraft), erlaubt das Omega-Modell Bitcoin-Investoren, ihre Positionen zu optimieren, um das "obere Ende" der Verteilung zu maximieren. Durch das Hinzufügen von eins zum Verhältnis der Nettorendite zum durchschnittlichen Verlust ermöglicht die Kapsos-Formel Algorithmen, schnell und effizient die Gewichte (𝑤) zu finden, die die beste Wahrscheinlichkeit des Erfolgs im Verhältnis zu den individuellen Zielen der Investoren bieten.
4. Vergleichende Analyse: Bitcoin vs. S&P 500
Um den wahren Wert des Omega-Verhältnisses zu verstehen, ist es notwendig, Bitcoin mit einem traditionellen Benchmark wie dem S&P 500-Index zu vergleichen. Traditionelle Risikometriken wie die Standardabweichung versagen hier oft, da sie die Asymmetrie und Unterschiede in den "Schwanz"-Strukturen der beiden Verteilungen nicht berücksichtigen.
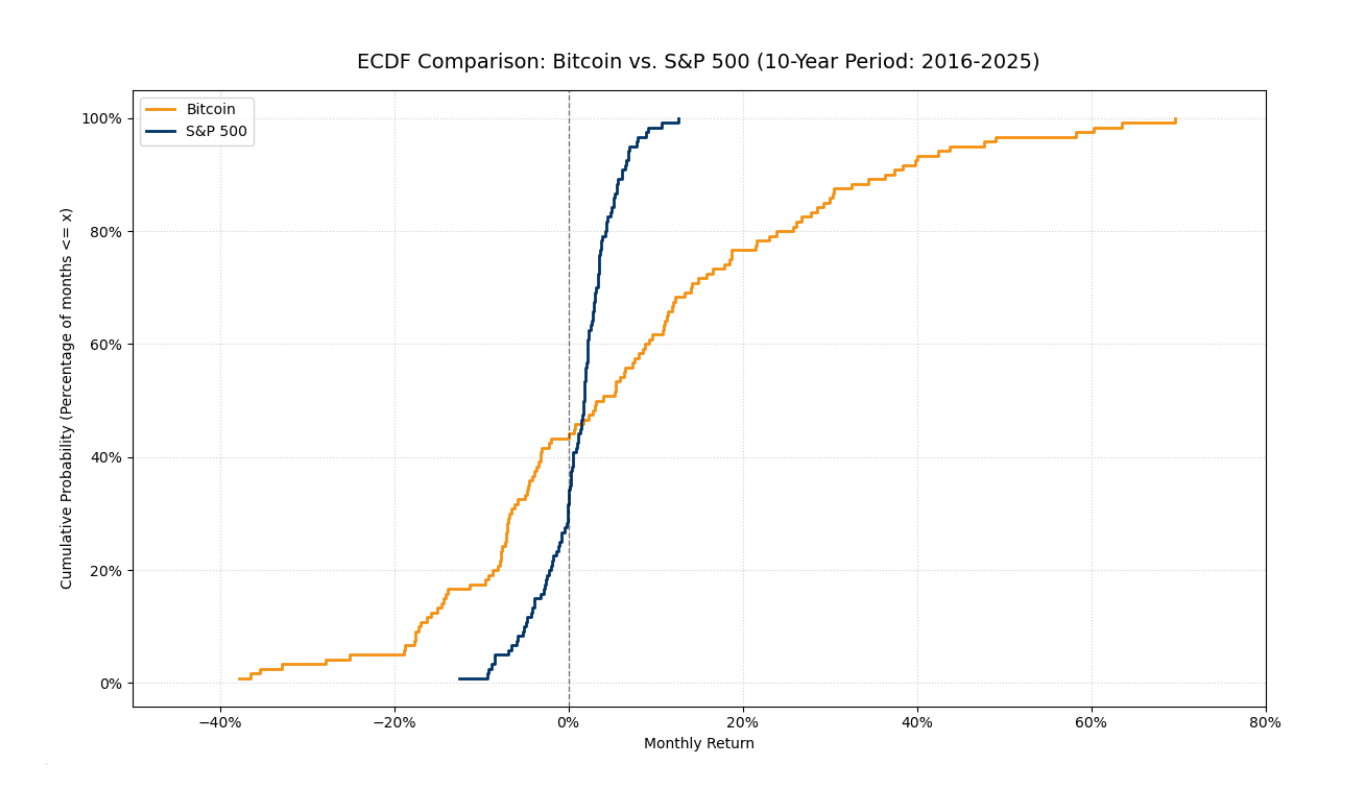
Dieses vergleichende ECDF-Diagramm veranschaulicht den grundlegenden Unterschied zwischen den beiden Assets:
Konzentration vs. Volatilität: Die S&P 500-Linie (dunkelblau) ist deutlich steiler und konzentriert sich in einem engen Bereich um null. Dies deutet auf ein Asset mit geringerer Volatilität und einer engeren, vorhersehbareren Verteilung hin.
Bitcoins "Fat Tails": Die Bitcoin-Linie (orange) zeigt deutlich breitere Extreme. Dies ist ein visuelles Zeichen für "fat tails"—eine höhere Wahrscheinlichkeit für massive negative und positive Abweichungen im Vergleich zum traditionellen Markt.
Leistungsdetails: Während der schlimmste Monat von Bitcoin -37,77 % erreichte, generierte das Asset erfolgreich explosive Wachstumsperioden von bis zu +69,63 %. Diese asymmetrischen Sprünge im "rechten Ende" sind der Grund, warum Bitcoin oft ein viel höheres Omega-Verhältnis bei niedrigeren MAR-Niveaus generiert.
Fazit: Der Vergleich bestätigt, dass Omega eine fairere Risikometrik als die Standardabweichung ist. Es erkennt das hohe Potenzial von Bitcoin an, ohne dessen "fat tail"-Eigenschaften zu ignorieren, und ermöglicht es den Anlegern, die Optimierungsformel anzuwenden, um die Portfolio-Gewichte (𝑤) im Verhältnis zu einer gewünschten Rendite-Schwelle (𝞃) auszubalancieren.
Abschlussfolgerung
Die Analyse über das Omega-Verhältnis beweist, dass traditionelle Metriken wie das Sharpe-Verhältnis für Assets mit "fat tails" wie Bitcoin unzureichend sind. Während ein einjähriger Zeitraum irreführend sein kann, zeigt der 10-Jahres-Horizont die statistische Dominanz der Gewinne (Ω = 1,621). Selbst bei einer hohen Schwelle von MAR = 5 % behält das Asset seine Effizienz (Ω = 1,2102) aufgrund der Größe seiner positiven Ausreißer. Der Vergleich mit dem S&P 500 hebt hervor, dass Bitcoin eine einzigartige Exposition gegenüber dem "rechten Ende" der Verteilung bietet. Die Nutzung des Modells von Kapsos et al. verwandelt diese theoretischen Einblicke in ein praktisches Werkzeug zur Portfoliooptimierung durch lineare Programmierung. Letztendlich bietet das Omega-Verhältnis eine ehrlichere und anpassungsfähigere Bewertung des Risikos und erkennt das Potenzial für explosives Wachstum an.
Literaturverzeichnis
Kapsos, M., Zymler, S., Christofides, N., und Rustem, B. (2011). Optimierung des Omega-Verhältnisses durch lineare Programmierung. Imperial College London.