Wie zk-ASM ein sicheres und vertrauenswürdiges Internet ermöglichen kann
Ursprüngliche Forschungsanalyse von Web3.com Ventures
0xFishylosopher
Hinweis: Dieser Artikel ist technisch recht anspruchsvoll und setzt grundlegende konzeptionelle Kenntnisse mit zk-Proofs und/oder zk-Rollups voraus. Eine allgemeinere Einführung in diese Prinzipien finden Sie hier.

Einführung
Zero Knowledge Proofs, insbesondere zk-SNARKs (Succinct Non-interactive Arguments of Knowledge), sind vielleicht eine der wichtigsten Technologien an den Grenzen von Web 3. Während die meiste Medienaufmerksamkeit und Aufmerksamkeit in diesem Teilbereich auf zk-Rollups gerichtet ist, Skalierungslösungen, die L1-Blockchains wie Ethereum um ein Vielfaches skalierbarer machen, ist dies bei weitem nicht die einzige Anwendung von zk-SNARKs. In diesem Essay werde ich das Konzept von Zero-Knowledge Assembly Code (oder zkASM) eingehend analysieren, seine Anwendungsfälle sowohl in zk-Rollups als auch darüber hinaus bewerten und seine theoretischen Möglichkeiten zur Neuerfindung des Internets, wie wir es kennen, erkunden.
Technische Grundlagen
zk-ASM enthält, wie der Name schon sagt, zwei technische Hauptteile: ZK und ASM. Der ZK-Teil bezieht sich auf zk-SNARKs oder Succinct Non-Interactive Arguments of Knowledge, während sich der ASM-Teil auf Assemblercode bezieht. Um das Potenzial von zk-ASM zu verstehen, müssen wir zunächst die theoretischen Grundlagen dieser beiden scheinbar geheimnisvollen Konzepte verstehen.
zk-SNARKs
zk-SNARKs sind die Kronjuwelen der zk-Proofs: Sie sind ein prägnanter Beweis dafür, dass eine bestimmte Aussage wahr ist, wobei der Beweis nichts über die zu beweisenden Daten verrät. Stellen Sie sich beispielsweise vor, jemand behauptet die Aussage „Ich kenne ein m, sodass C(m) = 0“, wobei m eine Gigabyte lange Nachricht und C eine Funktion ist. Ein zk-SNARK wäre ein sehr kurzer Beweis (< 1 GB), der schnell überprüft werden kann und bei dem nichts über m verraten wird (außer öffentlich verfügbaren Informationen) [1].
Was ist also dieses „C(m)“? Wozu ist es nützlich? Diese Funktion ist eigentlich ein Rechenschaltkreis oder eine DAG-Darstellung (Directed Acyclic Graph) einer bestimmten Funktion, die wir ausführen möchten, wie das Diagramm zeigt [2]. Das „m“ sind im Wesentlichen die Eingangsdaten in den Schaltkreis, und bestimmte „Knoten“ in dem Schaltkreis sind einzelne Logikgatter oder Rechenoperationen. Beispielsweise kann ein „+“-Knoten „2“ und „3“ als Eingänge haben und eine „5“ an den nächsten Operator ausgeben. Somit kann eine beliebige Rechen- oder Logikoperation in einem „Rechenschaltkreis“ kodiert werden.
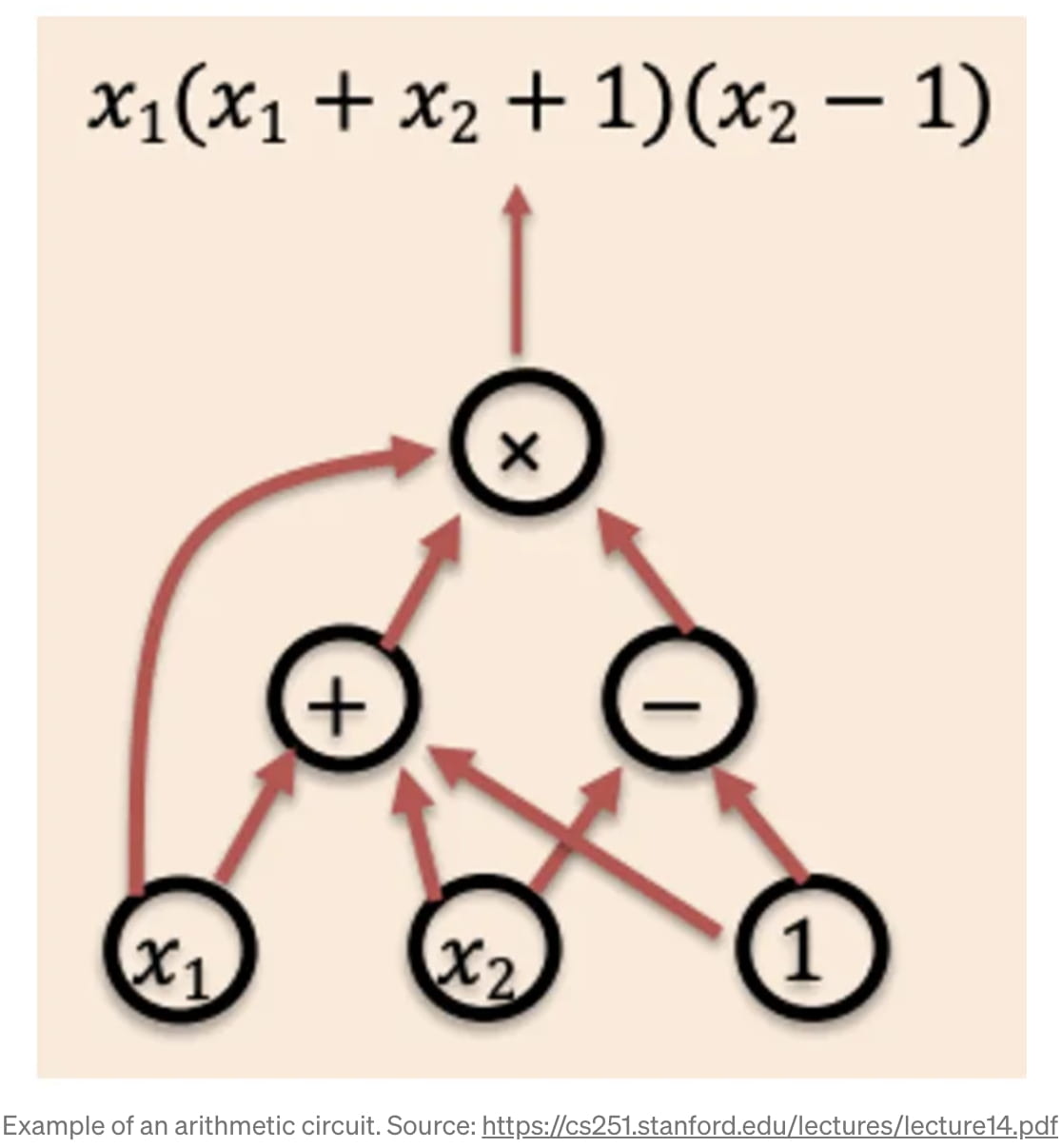
Sobald wir diese Rechenschaltung als Darstellung des Codes haben, auf dem wir einen zk-SNARK ausführen möchten, können wir mit dem Aufbau dieses zk-SNARK beginnen. Grundsätzlich ist ein zk-SNARK aufgrund des „Fundamentalsatzes der Algebra“ möglich, der besagt, dass ein Polynom vom Grad „d“ höchstens „d“ Wurzeln hat [3]. Der mathematische Trick besteht aus zwei Schritten: (1) die Funktion „f(m)“, die wir beweisen möchten, irgendwie in ein Polynom umzuwandeln (und dabei zu bleiben) und (2) den „Fundamentalsatz der Algebra“ zu verwenden, um mit dem Polynom zu interagieren und einen prägnanten Beweis zu liefern. Im Fachjargon wird der erste Teil als „Polynomial Commitment Scheme“ (PCS) und der zweite Teil als „Polynomial Interactive Oracle Proof“ (PIOP) bezeichnet [4].
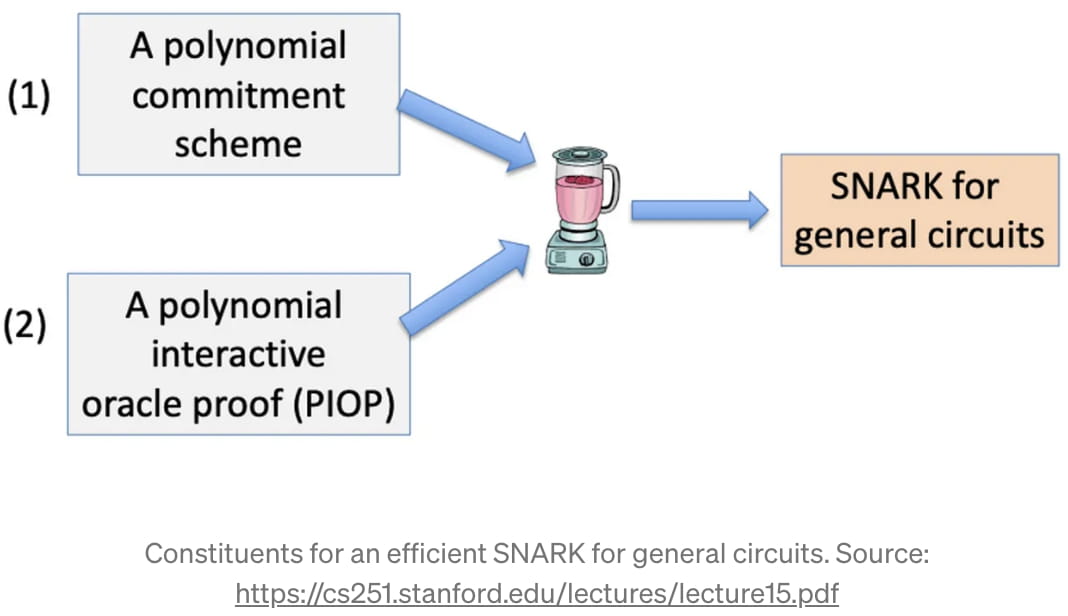
Während die spezifischen Implementierungen eines PCS und PIOP über den Rahmen dieses Artikels hinausgehen, haben wir bisher eine grobe Skizze für die Kernschritte eines zk-SNARK erstellt:
Sie haben eine Funktion Ihrer Wahl (Codefunktion, mathematische Gleichung usw.), mit der Sie einen zk-SNARK ausführen möchten
Kodieren Sie diese Funktion als Rechenschaltung C(m)
Führen Sie ein PCS aus, um eine polynomische Darstellung dieser Rechenschaltung zu erhalten
Führen Sie ein PIOP aus, um einen prägnanten Beweis zu erhalten, dessen Größe logarithmisch zum ursprünglichen „m“ ist.
Und voilà, wir haben ein maßgeschneidertes zk-SNARK, das beweisen kann, dass jemand eine bestimmte Nachricht kennt, ohne preiszugeben, um welche Nachricht es sich handelt.
Baugruppencode
Das zweite Puzzleteil von zk-ASM ist die Idee des Assemblercodes. Assemblercode ist eine Klasse von Sprachen, die sehr einfache Anweisungen enthalten, die für eine Maschine leicht zu lesen, für einen Menschen jedoch ziemlich schwer zu entziffern sind. Im Gegensatz zu höheren Programmiersprachen wie Python, Java oder sogar C enthalten Assemblersprachen sehr primitive Funktionen wie Verschieben, Vergleichen, Addieren und Springen in einer Reihe von Datenregistern auf dem Prozessor und fest codierten Speicherorten. Der Python-Code zum Drucken der Zahlen 1 bis 9 auf dem Bildschirm lautet beispielsweise 123456789:

Ziemlich einfach zu verstehen, oder? Hier ist die x86-Assembler-Version davon [5]:

Sehr viel komplizierter, insbesondere für eine so einfache Operation. Warum also überhaupt Assemblersprache verwenden? Wie oben erwähnt, sind diese Anweisungen zwar für einen Menschen nicht leicht zu lesen, aber sie lassen sich sehr einfach in den 110011001 Bytecode „assemblieren“, damit eine Maschine sie lesen und ausführen kann (dies wird als Assembler bezeichnet) [6]. Höhere Sprachen wie Python und Java sind vergleichsweise viel benutzerfreundlicher zu lesen, aber in diesen Sprachen geschriebene Programme können nicht direkt von einem Prozessor ausgeführt werden. Stattdessen sind wir auf einen „Compiler“ angewiesen, der den von uns geschriebenen Python- oder Java-Code durcharbeitet und einen Dump an Assemblercode wie den oben gezeigten ausspuckt, der von der Maschine assembliert und ausgeführt werden kann. Wir können davon ausgehen, dass dasselbe Stück Python oder Java reibungslos auf verschiedenen Prozessoren und verschiedenen Betriebssystemen läuft, da der Compiler die Schwerstarbeit übernimmt und Ihren Quellcode in eine für den jeweiligen Prozessor oder das jeweilige Betriebssystem spezifische Assemblersprache kompiliert.
Da alle Sprachen zu Assemblercode kompiliert werden (der wiederum zu ausführbaren Binärdateien kompiliert wird), ist Assembler im Wesentlichen wie die „Mutter aller Sprachen“. Nehmen wir nun an, wir können alle Operanden in einer Assemblersprache (wie x86 oder RISC-V) in eine arithmetische Schaltkreisdarstellung umwandeln, sodass wir zk-SNARK-Beweise für alle Operanden in dieser Assemblersprache liefern können. Das bedeutet, dass wir theoretisch in der Lage sind, einen zk-SNARK für jedes Programm zu liefern, das in einer beliebigen höheren Programmiersprache (wie Python oder Java) geschrieben ist und in diese Assemblersprache kompiliert wird. Und deshalb müssen wir uns Gedanken über zk-ASMs machen.
Praktische Anwendungen
zk-EVM-Rollups: Polygon zk-ASM
Eine der wichtigsten Anwendungen für zk-ASM ist die Erstellung von Ethereum Virtual Machine-kompatiblen zk-Rollups oder zk-EVMs. Ein zk-EVM ist für die Skalierbarkeit der Blockchain unglaublich wichtig, da es Programmierern ermöglicht, auf einer zk-Rollup-basierten L2-Kette zu implementieren, ohne viel (wenn überhaupt) ihres Codes zu ändern [7]. In diesem Bereich ist Polygons zk-EVM eine beispielhafte Fallstudie, die zeigt, wie zk-ASM verwendet werden kann, um dieses Ziel zu erreichen.
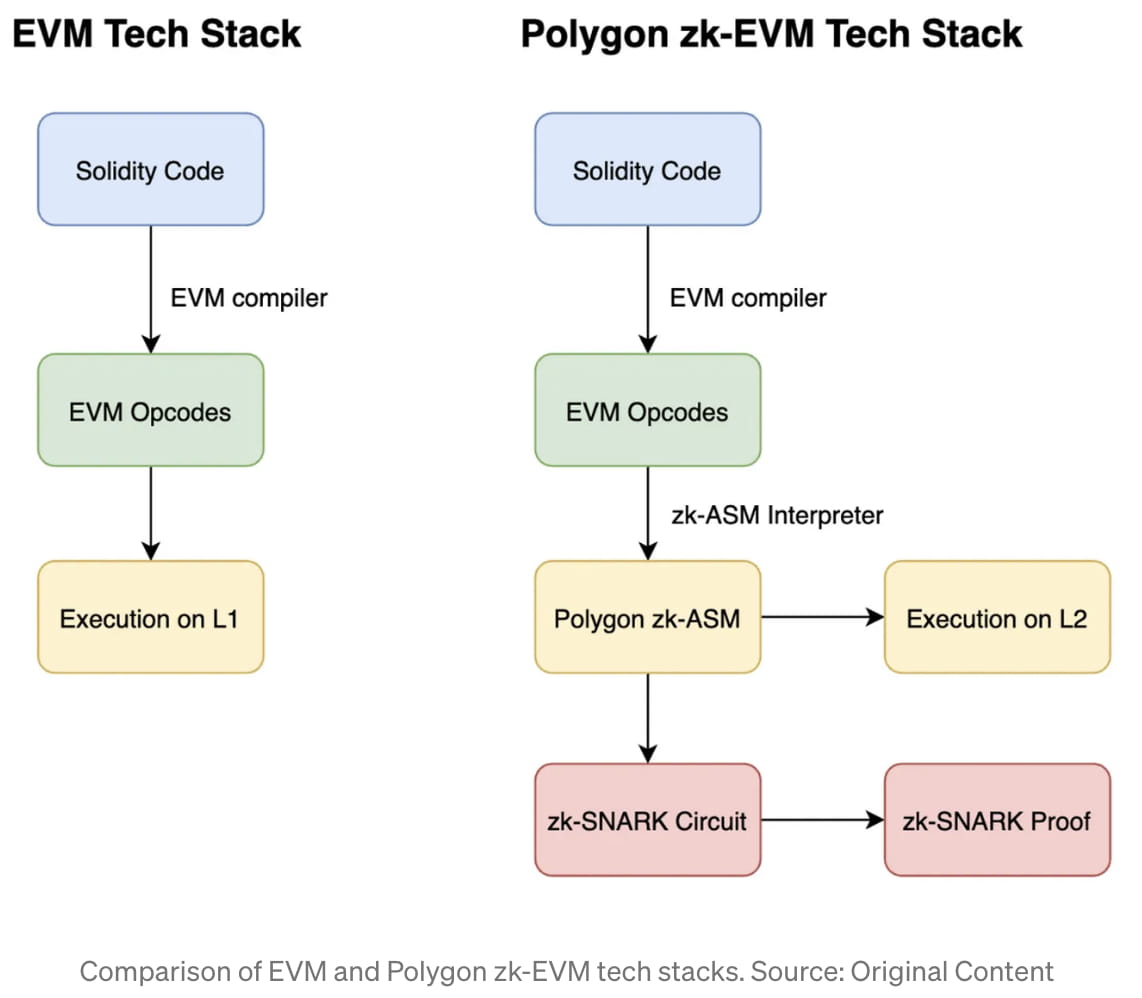
Wenn Programmierer auf der Ethereum L1-Blockchain entwickeln, programmieren sie normalerweise in Solidity, einer C-ähnlichen Hochsprache. Dieser Solidity-Code wird in eine Reihe von EVM-Opcodes wie ADD, SLOAD und EQ kompiliert, bevor er auf der L1-Blockchain ausgeführt wird [8]. Standardmäßig erstellt dieser Prozess offensichtlich keine Art von zk-Proof. Polygons Trick besteht darin, eine Methode zu erstellen, um jeden der EVM-Opcodes in ihr benutzerdefiniertes zk-ASM zu interpretieren, das sehr zk-SNARK-freundlich ist. Dann führt ihr L2-zk-EVM das zk-ASM aus und erstellt gleichzeitig eine zk-SNARK-Schaltung des ASM, um einen zk-SNARK-Beweis zu erstellen [9]. Beispielsweise wird der ADD-Opcode im EVM wie folgt in Polygons zk-ASM übersetzt [10]:

Da der Taschenspielertrick von Polygon zk-EVM auf Assemblerebene stattfindet, ist er zwei Ebenen vom Code entfernt, den der durchschnittliche Ethereum-Programmierer berührt, nämlich auf der „Solidity“-Ebene. Aus diesem Grund können die meisten Entwickler ihren für das Ethereum-Mainnet erstellten EVM-Code direkt auf das Polygon zk-EVM portieren. Da Polygon zk-EVM den Tech-Stack von Ethereum bis auf die Opcode-Ebene „hält“, bleibt außerdem die gesamte Debugging-Infrastruktur, die auf der Analyse kompilierter Opcodes basiert, nutzbar und intakt. Dies ist anders als bei einigen anderen zk-EVM-Designs, wie zk-Sync, das keine zk-Proofs auf Opcode-Ebene bereitstellt. Obwohl Polygon seine eigene Assemblersprache erfindet und beweist, schreibt Vitalik, dass es „immer noch EVM-Code verifizieren kann, es verwendet dazu nur eine andere interne Logik“ [11].
Mehr als Rollups: zk-WASM
zk-EVMs sind keineswegs die einzige Anwendung für zk-ASMs. Erinnern Sie sich an unsere vorherige Behauptung, dass Assemblersprachen im Wesentlichen „die Mutter aller Sprachen“ sind und dass die Erstellung eines zk-ASM zk-Proofs für generische Programme freischalten wird, die in jeder Sprache geschrieben sind, die in diese Assemblersprache kompiliert werden kann. Web Assembly oder WASM ist eine der wichtigsten neuen Assemblersprachen. WASM wurde erstmals 2018 veröffentlicht und zielt darauf ab, eine Assemblersprache zu erstellen, die die Ausführungsgeschwindigkeit von Web-Apps erhöht und eine Ausführungsergänzung zu Javascript bietet, der primären Programmiersprache hinter dem Web [12].
Im Wesentlichen hat die wachsende Größe und Komplexität von Web-Apps im Laufe der Jahre dazu geführt, dass Browser oft unglaublich langsam sind, um alles zu kompilieren, was in Javascript geschrieben ist, und auf komplexe Zyklen aus Kompilieren, Optimieren und Neuladen angewiesen sind [12]. WebAssembly hingegen macht die Abhängigkeit von komplexen Browser-Ausführungs-Engines überflüssig, indem es eine portable, modulare und leicht ausführbare Assemblersprache bereitstellt. Darüber hinaus ermöglicht WASM als Assemblersprache Programmierern, Code-Schnipsel direkt in C, C++, Rust, Java oder Ruby zu schreiben, die nativ in einem Browser ausgeführt werden. WASM ist daher zu einer Technologie der Wahl für die „Bereitstellung verteilter serverloser Funktionen“ geworden [13].
Warum und wie kommen also zk-SNARKs ins Spiel? WASM ist insofern einzigartig, als es sich um eine clientseitige Technologie handelt, die direkt mit Benutzereingaben und -daten interagieren kann. Da es sich dabei oft um sensible Daten wie Passwörter und persönliche Informationen handelt, benötigen wir eine Technologie, die (1) sicherstellt, dass das Programm korrekt ausgeführt wird, und dass (2) unsere sensiblen Informationen nicht verloren gehen. Wie oben beschrieben, ist ein zk-SNARK eine perfekte Lösung, um diese beiden Probleme zu lösen, und ist somit ein wichtiges Puzzleteil bei der Absicherung von WASM [14].
Während die Arbeit an der Entwicklung von zk-WASM noch in den Kinderschuhen steckt, gab es in letzter Zeit einige Projekte, die Prototypen von zk-SNARK-Schaltungen für WebAssembly veröffentlicht haben. Beispielsweise bietet der „ZAWA“-zk-SNARK-Emulator von Delphinus Lab eine Methode zum Kodieren der Operanden und Semantik einer WASM-virtuellen Maschine in eine arithmetische Schaltung, die es ermöglicht, zk-SNARK-Beweise durchzuführen [13]. Im Laufe der Zeit werden zk-WASM-Schaltungen zweifellos kontinuierlich optimiert, sodass Programme, die in generischen Sprachen (wie C, C++, Rust und Ruby) geschrieben sind, das Paradigma von zk-Proofs übernehmen können.
Abschluss
In diesem Essay haben wir die theoretischen Grundlagen von zk-ASM untersucht und zwei paradigmatische Fallstudien zu zk-ASM untersucht: Polygons Verwendung von zk-ASM zur Erstellung eines zk-EVM auf Opcode-Ebene sowie die Anwendung von zk-SNARKs auf WebAssembly zur Erstellung von zk-WASM. Letztendlich besteht das Versprechen von zk-ASM darin, die Interoperabilität und Skalierbarkeit von Web 2 mit der Vertrauenslosigkeit und Sicherheit von Web 3 zu vereinen.
Einerseits versuchen Blockchains zunehmend, ihre aktuellen Durchsatzengpässe zu überwinden und die Ausführung potenziell zu unterstützen, während andererseits Web 2-Methoden zunehmend in die Kritik geraten, weil sie Benutzerdaten und Privatsphäre unzureichend schützen. Da Programmierer in der Lage sind, Web 3-Designparadigmen in ihrem Web 2-Code anzuwenden und Web 2-Sprachen und -Code in die Blockchain einzuführen, könnten generische zk-ASMs einen Schnittpunkt in der Welt von Web 2 und Web 3 darstellen [15]. In diesem Sinne könnte zk-ASM es uns ermöglichen, uns ein sichereres und vertrauenswürdigeres Internet vorzustellen.
🐦 @0xfishylosopher
📅 17. Dezember 2022
Haftungsausschluss: Die oben dargestellten Informationen dienen ausschließlich zu Bildungszwecken und stellen keine Finanzberatung dar. Sie spiegeln ausschließlich die Ansichten des Autors wider. Delphinus Lab ist ein Portfoliounternehmen von Web3.com Ventures.
Verweise
[1] https://z.cash/technology/zksnarks/
[2] https://cs251.stanford.edu/lectures/lecture14.pdf
[3] https://www.britannica.com/science/fundamental-theorem-of-algebra
[4] Aufbau effizienter SNARKs: https://cs251.stanford.edu/lectures/lecture15.pdf
[5] Beispiel von: https://www.tutorialspoint.com/assembly_programming/assembly_loops.htm
[6] https://en.wikipedia.org/wiki/Assemblersprache
[7] https://www.alchemy.com/overviews/zkevm
[8] Liste der Opcodes: https://ethereum.org/en/developers/docs/evm/opcodes/
[9] https://wiki.polygon.technology/docs/zkEVM/zkASM/introduction
[10] https://wiki.polygon.technology/docs/zkEVM/zkASM/some-examples
[11] https://vitalik.ca/general/2022/08/04/zkevm.html
[12] https://blog.developer.adobe.com/understanding-webassembly-wasm-d5b592208ecc
[13] https://jhc.sjtu.edu.cn/~hongfeifu/manuscriptb.pdf
[14] https://hyperoracle.medium.com/zkwasm-the-next-chapter-of-zk-and-zkvm-471038b1fba6
[15] https://delphinuslab.com/zk-wasm/